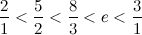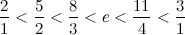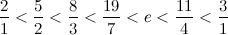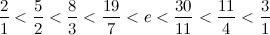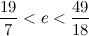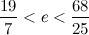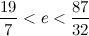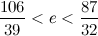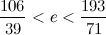С нового учебного года я начал читать два интересных блога по русскому языку. Блог ученика
Мир глазами человека и блог учителя
Оно вам надо!
В ученическом блоге даются советы по подготовке к олимпиаде "Русский медвежонок", объясняются некоторые неочевидные правила, публикуются новости из других областей науки. Почитав же учительский блог, я тоже узнал много нового и искренне обрадовался за учеников, с которыми работает такой замечательный педагог, как его автор.
Так вот, на днях я вспомнил об одной задаче, лежащей на стыке языка и математики. Когда-то мы вместе с форумчанами
Назвы и
Смекалки искали
самоописывающие выражения, то есть такие, количество букв в словесном описании которых равно их числовому значению. Как, например, в слове "
три" ровно 3 буквы, а во фразе "
два в кубе" букв 8.
После дальнейшего размышления оказалось, что есть способ построить подобное выражение для любого натурального числа, большего семи.
два в кубе = 8
трижды три = 9
дважды пять = 10
одиннадцать = 11
трижды четыре = 12
три плюс десять = 13
пять плюс девять = 14
треть сорока пяти = 15
восемь плюс восемь = 16
два плюс пятнадцать = 17
А теперь воспользуемся тем, что во фразе "плюс десять" ровно 10 букв и будем добавлять её к предыдущим выражениям:
два в кубе плюс десять = 18
трижды три плюс десять = 19
дважды пять плюс десять = 20
одиннадцать плюс десять = 21
......
дважды пять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять = 100
......
Кстати, в англоязычной занимательной математике используется название "
честные числа" (
honest numbers). Там честными оказались числа 4, 8, 10, 11 и все, большие двенадцати.
Да, задача решена. Но не стало ли немного грустно от того, что решение оказалось таким простым и однообразным?
Чтобы продолжить наши математические развлечения, можно попробовать подбирать примеры, в которых бы не использовался плюс или в которых одно математическое действие не использовалось бы более раза.
Тогда выходит намного интереснее:
восьмое простое число = 19
антье корня из шестиста пяти = 24
логарифм десятичный ста дециллионов = 32
Приглашаю продолжить и заполнить пробелы!
По тегу "
самоописывающее" в блоге можно найти много других интересных конструкций, как математических, так и языковых..






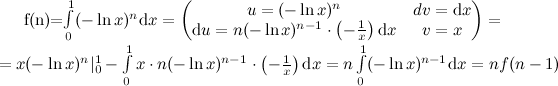
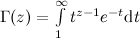
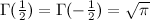
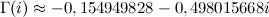




 , то после n бросков оно не наступит с вероятностью
, то после n бросков оно не наступит с вероятностью 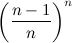 . Соответственно, шансы положительного исхода серии из n опытов составят
. Соответственно, шансы положительного исхода серии из n опытов составят 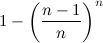
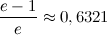
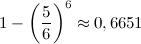 мало отличается от этой.
мало отличается от этой.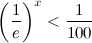
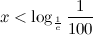
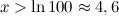
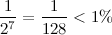
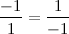
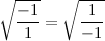
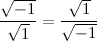
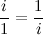
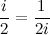
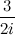 , получим:
, получим: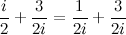
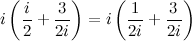
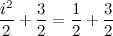
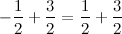
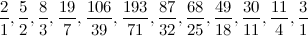
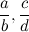 , произведения ad и bc отличаются на 1.
, произведения ad и bc отличаются на 1.