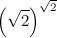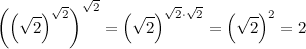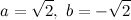2011 - простое число. Поэтому оно представляется в виде разности квадратов натуральных чисел единственным образом: 20112=10062-10052
Желаем вам, чтобы в новом году все задачи решались просто и легко :)
Интересные числа, занимательные математические факты и удивительные конструкции. Узнавайте каждый день что-то новое!
пятница, 31 декабря 2010 г.
четверг, 30 декабря 2010 г.
Самый длинный месяц
Самый длинный месяц у нас - это октябрь.Из-за перевода часов он на час длиннее остальных месяцев, в которых по 31 дню.
среда, 29 декабря 2010 г.
Формула площади
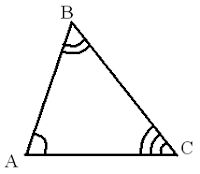
Площадь треугольника можно вычислить, зная его углы и радиус описанной окружности по формуле:
S=2R2sin A sin B sin C
четверг, 23 декабря 2010 г.
среда, 22 декабря 2010 г.
Делимость на 3 и 9
Читатель нашего блога segagenesis предложил в качестве темы признаки делимости на 3 и 9. Если сумма цифр в числе кратна трём, то это число делится на три. тоже самое и для девятки.
Почему это работает?
Пусть у нас есть (n+1)-значное число anan-1...a5a4a3a2a1a0. Его можно записать как an10n+an-110n-1+...+a5105+a4104+a3103+a2102+a110+a0=
=an(999...999+1)+an-1(999...99+1)+...+a5(99999+1)+a4(9999+1)+a3(999+1)+a2(99+1)+a1(9+1)+a0=
=999...999an+999...99an-1+...+99999a5+9999a4+999a3+99a2+9a1+
+an+an-1+...+a5+a4+a3+a2+a1+a0
Поскольку все слагаемые, в которых есть множитель, состоящий из девяток, делятся на 9, то делится или не делится исходное число на 9 или на 3 зависит только от того, делится ли на 9 или на 3 сумма его цифр.
Почему это работает?
Пусть у нас есть (n+1)-значное число anan-1...a5a4a3a2a1a0. Его можно записать как an10n+an-110n-1+...+a5105+a4104+a3103+a2102+a110+a0=
=an(999...999+1)+an-1(999...99+1)+...+a5(99999+1)+a4(9999+1)+a3(999+1)+a2(99+1)+a1(9+1)+a0=
=999...999an+999...99an-1+...+99999a5+9999a4+999a3+99a2+9a1+
+an+an-1+...+a5+a4+a3+a2+a1+a0
Поскольку все слагаемые, в которых есть множитель, состоящий из девяток, делятся на 9, то делится или не делится исходное число на 9 или на 3 зависит только от того, делится ли на 9 или на 3 сумма его цифр.
воскресенье, 19 декабря 2010 г.
495
Как мы уже писали, число 6174 является неподвижной точкой преобразования Капрекара для четырёхзначных чисел.
Для трёхзначных же таковым является число 495. Берём любое 3-значное число и из его цифр составляем 2 числа: с цифрами, идущими по возрастанию и идущими по убыванию. Затем вычитаем из первого второе.
512:
521-125=396
963-369=594
954-459=495
А вот для преобразований 5-значных чисел неподвижных точек нет.
четверг, 16 декабря 2010 г.
Расстояние между степенями
Существует ровно 3 пары натуральных чисел, одно из которых является степенью двойки, а другое - степенью тройки, расстояние между которыми равно 1.
Это 1 и 2; 2 и 3; 8 и 9.
Это 1 и 2; 2 и 3; 8 и 9.
вторник, 14 декабря 2010 г.
2
2 - единственное чётное простое число. Иногда это свойство называют незначительным, потому что тогда для любого простого p - это единственное простое, делящееся на p.
Однако свойства чётности чисел применяется в намного большем круге задач, нежели делимость на какое-нибудь другое число. И, кроме того, все нечётные, т.е. не делящиеся на 2 числа дают одинаковый остаток. Этого нельзя сказать ни про какое другое число.
Однако свойства чётности чисел применяется в намного большем круге задач, нежели делимость на какое-нибудь другое число. И, кроме того, все нечётные, т.е. не делящиеся на 2 числа дают одинаковый остаток. Этого нельзя сказать ни про какое другое число.
воскресенье, 12 декабря 2010 г.
пятница, 10 декабря 2010 г.
Коммутативность
С первого класса мы учим, что "от перемены мест слагаемых сумма не меняется". По научному такое свойство операции сложения называется коммутативностью. a+b=b+a.
Коммутативно и умножение действительных (да и комплексных) чисел: axb=bxa. А вот операция возведения в степень - некоммутативна. К примеру, 32=9, а 23=8.
Коммутативно и умножение действительных (да и комплексных) чисел: axb=bxa. А вот операция возведения в степень - некоммутативна. К примеру, 32=9, а 23=8.
четверг, 9 декабря 2010 г.
Логарифм
Человек воспринимает ощущения не пропорционально величине раздражителя, а пропорционально его логарифму. Так, например, субъективное различие между грузами в 1 кг и 2 кг будет таким же, как между 2 кг и 4 кг.
понедельник, 6 декабря 2010 г.
Перекладывание карт
Рассмотрим колоду из N карт с номерами от 1 до N. если номер верхней карты равен K, поменяем порядок K верхних карт на обратный. Будем поступать так, пока на верх не выйдет единица.
Для 5 карт дольше всего перекладываний (7) будет для колоды 3, 1, 4, 5, 2
31452
41352
53142
24135
42135
31245
21345
12345
Для 5 карт дольше всего перекладываний (7) будет для колоды 3, 1, 4, 5, 2
31452
41352
53142
24135
42135
31245
21345
12345
воскресенье, 5 декабря 2010 г.
Перестановка цифр
Т.к. это 185-й пост, я захотел найти что-то интересное про это число в Энциклопедии целочисленных последовательностей. Там наткнулся на любопытную последовательность, членом которой оно является. Последовательность строится так:
Начнём с единицы. Каждое следующее число будем получать, прибавив 4 к предыдущему числу, записанному в обратном порядке. Таким образом, из 1 получим 1+4=5, далее 5+4=9, 9+4=13, 31+4=35, 53+4=57, 75+4=79, 79+4=101, 101+4=105, 501+=505, 505+4=509, 905+4=909, 909+4=913, 319+4=323 и т.д.
56-й член данной последовательности снова будет равен пяти и она зациклится.
Интересно, существуют ли последовательности, построенные по аналогичному правилу, но с прибавлением отличного от четвёрки числа, которые растут неограниченно? Мне пока кажется, что таких нет, но определённо, стоит ещё подумать об этом.
Начнём с единицы. Каждое следующее число будем получать, прибавив 4 к предыдущему числу, записанному в обратном порядке. Таким образом, из 1 получим 1+4=5, далее 5+4=9, 9+4=13, 31+4=35, 53+4=57, 75+4=79, 79+4=101, 101+4=105, 501+=505, 505+4=509, 905+4=909, 909+4=913, 319+4=323 и т.д.
56-й член данной последовательности снова будет равен пяти и она зациклится.
Интересно, существуют ли последовательности, построенные по аналогичному правилу, но с прибавлением отличного от четвёрки числа, которые растут неограниченно? Мне пока кажется, что таких нет, но определённо, стоит ещё подумать об этом.
суббота, 4 декабря 2010 г.
е в США
Оказывается, в США число е запоминают через президента Эндрю Джексона
Он избирался дважды (2), был седьмым президентом (7), избирался в 1828 году, это число повторяется дважды, т.к. он 2 раза был президентом, а затем идёт равнобедренный прямоугольный треугольник (459045).
Он избирался дважды (2), был седьмым президентом (7), избирался в 1828 году, это число повторяется дважды, т.к. он 2 раза был президентом, а затем идёт равнобедренный прямоугольный треугольник (459045).
пятница, 3 декабря 2010 г.
Сколько в году секунд
Если в году 365,25 суток, в сутках по 24 часа, в часе 3600 секунд, то в секунд в году 31 557 600. Для приближённых вычислений часто пользуются значением
По этому поводу есть шутка:
В году приблизительно пи на десять в седьмой секунд. Пи - потому что орбита круглая, в седьмой - потому что в неделе семь дней. А приблизительно - потому, что орбита на самом деле не идеально круглая, а эллиптическая.
По этому поводу есть шутка:
В году приблизительно пи на десять в седьмой секунд. Пи - потому что орбита круглая, в седьмой - потому что в неделе семь дней. А приблизительно - потому, что орбита на самом деле не идеально круглая, а эллиптическая.
среда, 1 декабря 2010 г.
Зима пришла!
Зима наступила, хочется снега, очень хочется. Ещё в начале года писал программу, которая для Windows XP заметает снегом рабочий стол. Самое главное, что отличает мою программу от аналогов - движение мыши создаёт потоки воздуха, которые увлекают снежинки за собой. Поэтому можно самостоятельно направлять рост снежных узоров, к примеру, создавая вихри, скатывая снежки и прикрепляя их в нужном месте.
Вот как выглядит окно после некоторого времени падения снежинок:
Скачать программу Interactive Desktop Snowfall for Windows XP, freeware, 600KB
вторник, 30 ноября 2010 г.
понедельник, 29 ноября 2010 г.
Одинаковые буквы
Буквы
Г, З, И, Л, М, П, С топологически одинаковы. Все они представляют собой согнутый отрезок без самопересечений.
Г, З, И, Л, М, П, С топологически одинаковы. Все они представляют собой согнутый отрезок без самопересечений.
воскресенье, 28 ноября 2010 г.
0
У цифры 0 есть две оси и один центр симметрии. В некоторых шрифтах этим свойством обладает и цифра 8, но в тех, где верхний кружок меньше нижнего, у неё всего-навсего одна ось симметрии.
суббота, 27 ноября 2010 г.
Форумная игра "Что? Где? Когда?"
На форуме умных людей Nazva.net пользователь Лев проводит игру "Что? Где? Когда?"
Ему удаётся создать атмосферу, максимально приближенную к телевизионной версии игры.Для участия в игре необходимо зарегистрироваться.
Вы можете по желанию занять сторону игроков или зрителей, в зависимости от того, хотите ли вы отвечать на вопросы или загадывать их.
В отличие от оригинальной игры, время на обсуждение вопроса составляет полчаса (30 минут), из-за учета особенностей форумной коммуникации. Оно может варьироваться в будущем.
Также отличие в том, что садиться за стол и вставать из-за него можно прямо посреди раунда.
Разумеется, под честное слово, в течение обсуждения запрещено пользоваться какими-либо иными источниками информации.
Очень рекомендую, если вам нравится загадывать или разгадывать интересные вопросы, принять участие! :)
Ему удаётся создать атмосферу, максимально приближенную к телевизионной версии игры.Для участия в игре необходимо зарегистрироваться.
Вы можете по желанию занять сторону игроков или зрителей, в зависимости от того, хотите ли вы отвечать на вопросы или загадывать их.
В отличие от оригинальной игры, время на обсуждение вопроса составляет полчаса (30 минут), из-за учета особенностей форумной коммуникации. Оно может варьироваться в будущем.
Также отличие в том, что садиться за стол и вставать из-за него можно прямо посреди раунда.
Разумеется, под честное слово, в течение обсуждения запрещено пользоваться какими-либо иными источниками информации.
Очень рекомендую, если вам нравится загадывать или разгадывать интересные вопросы, принять участие! :)
Air Traffic Control Arcade
Пишу новую флеш-игру - аркадный симулятор авиадиспетчера? попутно осваивая ActionScript 3.

На экран будут залетать самолёты, которые нужно провести до точек выхода.

Кроме опасности столкновения самих самолётов, мешать выполнить задание будут стаи птиц, грозы, ветер. Есть ещё пара нереализованных задумок.


На экран будут залетать самолёты, которые нужно провести до точек выхода.
Кроме опасности столкновения самих самолётов, мешать выполнить задание будут стаи птиц, грозы, ветер. Есть ещё пара нереализованных задумок.

среда, 24 ноября 2010 г.
Формулы перевода координат со сферы на плоскость
А вот и сами формулы перевода координат из системы широта-долгота в X-Y
Расстояние от точки с широтой B и долготой L до экватора откладывается на ось Y и равно широте в градусах, помноженной на длину одного градуса меридиана, т.е. на 111,2 км
Y=111,2*B
Расстояние от нулевого меридиана откладывается на ось X и равно долготе в градусах, помноженной на длину одного градуса параллели на широте точки. А та равна 111,2cosB
X=111,2*L*cos(B)
вторник, 23 ноября 2010 г.
Что бы это значило?
Ситуация:
Сидит человек за компьютером. Видно, что чем-то недоволен. Затем он перекрестил монитор, набрал что-то на клавиатуре, и, радостный, завершил работу.
На самом деле именно так со стороны выглядела ситуация, когда я писал программу перевода геодезических координат: широты и долготы на плоскость и забыл, какая из координат на какую ось отображается.
Сидит человек за компьютером. Видно, что чем-то недоволен. Затем он перекрестил монитор, набрал что-то на клавиатуре, и, радостный, завершил работу.
На самом деле именно так со стороны выглядела ситуация, когда я писал программу перевода геодезических координат: широты и долготы на плоскость и забыл, какая из координат на какую ось отображается.
понедельник, 22 ноября 2010 г.
воскресенье, 21 ноября 2010 г.
Геометрический паркет
Существует ровно 3 вида правильных многоугольников, которыми можно замостить плоскость: это правильный треугольник, четырёхугольник (квадрат) и шестиугольник.
суббота, 20 ноября 2010 г.
Умножение двузначного числа на 11
Чтобы двузначное число умножить на 11, сложите его первую и последнюю цифру. Если результат будет однозначным, впишите его между двумя цифрами первоначального числа, а если двузначным – прибавьте первую цифру результата к первой цифре первоначального числа, а вторую – впишите между цифрами.
Примеры:
45х11
Складываем 4+5=9. Поэтому результатом будет 495.
76х11
Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.
Математическое обоснование:
Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b
Примеры:
45х11
Складываем 4+5=9. Поэтому результатом будет 495.
76х11
Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.
Математическое обоснование:
Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b
четверг, 18 ноября 2010 г.
Простые близнецы
Хотя бесконечность множества простых чисел доказывается несложно, вопрос о конечности или бесконечности пар простых чисел-близнецов, т.е. таких, разность которых равна 2, до сих пор не решён.
вторник, 16 ноября 2010 г.
Сокращение вычислений
Чтобы проверить, является ли число простым, достаточно проверить делимость этого числа на все простые, не превосходящие корня из него.
Например, чтобы доказать простоту числа 101, достаточно показать, что оно не делится на 2, 3, 5 и 7.
Например, чтобы доказать простоту числа 101, достаточно показать, что оно не делится на 2, 3, 5 и 7.
понедельник, 15 ноября 2010 г.
Простое число на промежутке [n;2n]
Оказывается, между натуральным числом n, большем единицы, и удвоенным числом (2n) всегда найдётся простое число.
Эту теорему доказал Чебышев в 1850 году.
Эту теорему доказал Чебышев в 1850 году.
воскресенье, 14 ноября 2010 г.
n составных чисел подряд
Существуют сколь угодно длинные промежутки чисел, среди которых нет ни одного простого.
Например, все n чисел от (n+1)!+2 до (n+1)!+(n+1) - составные.
Например, все n чисел от (n+1)!+2 до (n+1)!+(n+1) - составные.
суббота, 13 ноября 2010 г.
1
По определению простого числа, у него ровно 2 делителя: 1 и само число.У составных же чисел делителей больше двух. Таким образом, число 1 - особенное, оно ни простое, ни составное.
четверг, 11 ноября 2010 г.
Простые числа в прогрессии
Любая арифметическая прогрессия с натуральными взаимно простыми первым членом и разностью включает бесконечное множество простых чисел.
среда, 10 ноября 2010 г.
Эвклидово доказательство бесконечности количества простых чисел
Допустим, простых чисел конечное количество. Но тогда, если их все перемножить, и прибавить единицу, получим число, которое не делится ни на одно из простых.
Вот на этом шаге часто, воспроизводя доказательство Эвклида, делают ошибку и говорят, что полученное число само является простым. Однако это не так: оно может быть или простым, или делящимся на некоторое простое число, большее максимального простого, входящего в произведение.
Действительно, числа
2+1=3
2*3+1=7
2*3*5+1=31
2*3*5*7+1=211
2*3*5*7*11+1=2311
- все простые, однако следующее:
2*3*5*7*11*13+1=30031 - составное, оно делится на 59.
Об этом математическом заблуждении, прочитав заметку о сумме иррациональных чисел, напомнил мне mmmkot.
Доказательство Эвклида очень хорошо иллюстрирует также принцип доказательства от противного: сначала мы предполагаем, что нечто верно, а затем показываем, к какому противоречию. приводит данное допущение.
Вот на этом шаге часто, воспроизводя доказательство Эвклида, делают ошибку и говорят, что полученное число само является простым. Однако это не так: оно может быть или простым, или делящимся на некоторое простое число, большее максимального простого, входящего в произведение.
Действительно, числа
2+1=3
2*3+1=7
2*3*5+1=31
2*3*5*7+1=211
2*3*5*7*11+1=2311
- все простые, однако следующее:
2*3*5*7*11*13+1=30031 - составное, оно делится на 59.
Об этом математическом заблуждении, прочитав заметку о сумме иррациональных чисел, напомнил мне mmmkot.
Доказательство Эвклида очень хорошо иллюстрирует также принцип доказательства от противного: сначала мы предполагаем, что нечто верно, а затем показываем, к какому противоречию. приводит данное допущение.
вторник, 9 ноября 2010 г.
Комплексное число в комплексной степени
А можно ли, возведя комплексное число в комплексную степень, получить действительное число?
Вот подсчитаем, чему равно ii
Для этого рассмотрим формулу Эйлера

Перенесём единицу вправо:
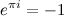
Теперь возведём левую и правую часть в степень i. Т.к. i2=-1, то
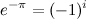
И теперь извлечём корень из левой и правой части:
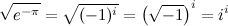
Таким образом,
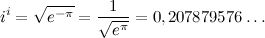
Итак, мнимое число во мнимой степени может давать действительный результат!
Вот подсчитаем, чему равно ii
Для этого рассмотрим формулу Эйлера
Перенесём единицу вправо:
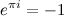
Теперь возведём левую и правую часть в степень i. Т.к. i2=-1, то
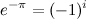
И теперь извлечём корень из левой и правой части:
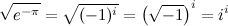
Таким образом,
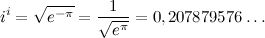
Итак, мнимое число во мнимой степени может давать действительный результат!
понедельник, 8 ноября 2010 г.
Иррациональная степень иррационального числа
А можно ли получить рациональное число, возведя иррациональное число в иррациональную степень?
Оказывается, тоже можно. Рассмотрим число
Если оно рационально, то задача решена. Если же нет (а на самом деле оно иррационально, но доказательство этого занимает солидный научный труд), то рассмотрим число
Которое является целым.
Оказывается, тоже можно. Рассмотрим число
Если оно рационально, то задача решена. Если же нет (а на самом деле оно иррационально, но доказательство этого занимает солидный научный труд), то рассмотрим число
Которое является целым.
воскресенье, 7 ноября 2010 г.
Сумма двух иррациональных чисел
При решении задач на доказательство рациональности/иррациональности некоторого выражения школьники часто высказывают заблуждение: "если числа a и b - иррациональны, то a+b - также иррационально".
То, что на самом деле сумма двух иррациональных чисел вполне может быть числом рациональным, и даже целым, можно показать, взяв
Тогда a+b=0
Тогда a+b=0
суббота, 6 ноября 2010 г.
Как ещё запомнить пи
Существует числовой стишок:
Надо только постараться и запомнить всё как есть — три, четырнадцать, пятнадцать, девяносто два и шесть.
Его указала в своём комментарии elka.
Есть ещё одна фраза, в которой количества букв в словах соответствуют цифрам:
Это я знаю и помню прекрасно: пи многие знаки мне лишни, напрасны
Надо только постараться и запомнить всё как есть — три, четырнадцать, пятнадцать, девяносто два и шесть.
Его указала в своём комментарии elka.
Есть ещё одна фраза, в которой количества букв в словах соответствуют цифрам:
Это я знаю и помню прекрасно: пи многие знаки мне лишни, напрасны
пятница, 5 ноября 2010 г.
Делимость на 7
Есть 164 шестизначных чисел, которые делятся на 7 при любом порядке своих цифр. Одно из них число 188111
Подробнее об этом - в решении задачи 3 Математических Маневров
Подробнее об этом - в решении задачи 3 Математических Маневров
четверг, 4 ноября 2010 г.
суббота, 30 октября 2010 г.
Куда переводят часы
Очень хорошее мнемоническое правило появилось пару лет назад на баше:
"Если за окном весна, которая начинается на букву В, то стрелки переводят на час вперёд. А еcли осень, с первой буквой О, то часы переводят обратно."
"Если за окном весна, которая начинается на букву В, то стрелки переводят на час вперёд. А еcли осень, с первой буквой О, то часы переводят обратно."
пятница, 29 октября 2010 г.
Пи в царской гимназии
Ученики в дореволюционной гимназии запоминали 11 знаков числа пи с помощью следующей фразы:
Кто и шутя и скоро пожелаетъ пи узнать, число ужъ знаетъ
3,1415926536
Можно ещё дополнительно запомнить, что вместо последней шестёрки идут 589
Кто и шутя и скоро пожелаетъ пи узнать, число ужъ знаетъ
3,1415926536
Можно ещё дополнительно запомнить, что вместо последней шестёрки идут 589
воскресенье, 24 октября 2010 г.
Lake Escape
Моя новая флеш-игра, которая иллюстрирует такую математическую задачу:
В центре круглого озера находится пловец. На берегу его поджидает гоблин, который бегает вчетверо быстрее, чем пловец плавает. Сможет ли пловец добраться до берега быстрее гоблина?
Эта задача имеет решение, проверить которое вы сможете, сыграв в игру Lake Escape. Просто двигайте курсор, чтобы указать направление движения. На первом уровне скорость гоблина всего втрое больше скорости пловца, и затем от уровня к уровню это отношение возрастает до трёх с четвертью, трёх с половиной, 3,75 и четырёх.
суббота, 23 октября 2010 г.
Что я знаю о кругах
Эта фраза помогает запомнить 5 знаков числа пи: соответствующие цифры равны количеству букв в словах.
Что (3) я (1) знаю (4) о (1) кругах (5)
Что (3) я (1) знаю (4) о (1) кругах (5)
четверг, 21 октября 2010 г.
15 знаков после запятой
Мы писали, как запомнить 9 знаков числа е после запятой.
Но достаточно легко запомнить и 15 его знаков.
е=2,718281828459045... и к году рождения Льва Толстого добавляются углы равнобедренного прямоугольного треугольника.
Но достаточно легко запомнить и 15 его знаков.
е=2,718281828459045... и к году рождения Льва Толстого добавляются углы равнобедренного прямоугольного треугольника.
среда, 20 октября 2010 г.
2010
Сейчас 20 часов 10 минут 20 числа 10 месяца 2010 года.
Два моих интернет проекта совершенно случайно начинались уже в замечательные даты: Этот блог стартовал в американский день числа пи, 3.14, а сайт "Приглашение в мир математики" начал свою работу в международный день числа пи, 22/7.
Под сегодняшнюю дату же я специально подгадал начало игры "Математические маневры", гибрида (надеюсь, жизнеспособного), пошаговой стратегии и олимпиады по математике.
Два моих интернет проекта совершенно случайно начинались уже в замечательные даты: Этот блог стартовал в американский день числа пи, 3.14, а сайт "Приглашение в мир математики" начал свою работу в международный день числа пи, 22/7.
Под сегодняшнюю дату же я специально подгадал начало игры "Математические маневры", гибрида (надеюсь, жизнеспособного), пошаговой стратегии и олимпиады по математике.
вторник, 19 октября 2010 г.
Математические маневры
В блоге Математическая задача недели завтра начнётся новое состязание, гибрид пошаговой стратегии и олимпиады по математике, Математические маневры. Сначала я случайно создал посты для проведения игры здесь а не там, затем удалил их, так что в РСС-ленте могут быть никуда не ведущие ссылки.
Компьютер в доказательстве
Проблема четырёх красок - первая серьёзная математическая теорема, доказательство которой и проверка доказательства были выполнены с помощью компьютера.
понедельник, 18 октября 2010 г.
Фантастика Гарднера
Про проблемы топологии есть два очень интересных фантастических рассказа Мартина Гарднера:
Нульсторонний профессор - об открытии поверхности вообще не имеющей сторон и
Остров пяти красок - об острове, на котором живёт 5 племён, причём каждые 2 племени имеют общую границу (более того - каждое племя имеет выход к морю).
Рекомендую :)
Нульсторонний профессор - об открытии поверхности вообще не имеющей сторон и
Остров пяти красок - об острове, на котором живёт 5 племён, причём каждые 2 племени имеют общую границу (более того - каждое племя имеет выход к морю).
Рекомендую :)
воскресенье, 17 октября 2010 г.
4 краски
Любую географическую карту можно раскрасить 4мя разными красками так, чтобы граничащие области были раскрашены в разные цвета.
суббота, 16 октября 2010 г.
Разрезание листа Мёбиуса
Собрался, наконец, сделать разбор файлов у себя на винчестере. И вот в папке Рассортировать/Для сортировки/Несортированное нашёл видео, с которым участвовал в конкурсе на сайте SmartVideos.ru.
Здесь показывается, как изготовить поверхность, у которой будет только одна сторона, и что случится, если её разрезать.
Здесь показывается, как изготовить поверхность, у которой будет только одна сторона, и что случится, если её разрезать.
пятница, 15 октября 2010 г.
дружественные числа
Дружественными называется пара натуральных чисел, каждое из которых является суммой делителей другого, меньших того. Наименьшая пара дружественных чисел была найдена ещё Пифагором, это 220 и 284.
1+2+4+5+10+11+20+22+44+55+110=284
1+2+4+71+142=220
1+2+4+5+10+11+20+22+44+55+110=284
1+2+4+71+142=220
четверг, 14 октября 2010 г.
Взаимоописывающие числа
Не существует шестизначного числа, аналогичного 6210001000 или 2020, в котором первая цифра указывает, сколько в числе нулей, вторая - сколько единиц и т.д. Но есть пара шестизначных чисел: 230100 и 311100.
Во втором числе 2 нуля, 3 единицы, 0 двоек, 1 тройка, 0 четвёрок и 0 пятёрок.
А в первом - 3 нуля, 1 единица, 1 двойка, 1 тройка, 0 четвёрок и 0 пятёрок.
Во втором числе 2 нуля, 3 единицы, 0 двоек, 1 тройка, 0 четвёрок и 0 пятёрок.
А в первом - 3 нуля, 1 единица, 1 двойка, 1 тройка, 0 четвёрок и 0 пятёрок.
среда, 13 октября 2010 г.
Магический квадрат с действиями
Магическими квадратами называются квадраты, в которых суммы чисел по горизонталям, вертикалям и диагоналям равны. Семёныч с форума Nazva.net нашёл квадраты иного рода, которые тоже можно назвать магическими:
В нём использованы все 9 цифр от 1 до 9, расставлены знаки действий, и результаты по горизонталям и диагоналям равны!
В нём использованы все 9 цифр от 1 до 9, расставлены знаки действий, и результаты по горизонталям и диагоналям равны!
вторник, 12 октября 2010 г.
Длина кривой Коха
Рассмотрим построение кривой Коха. На очередном шаге каждый отрезок заменяется на 4-звенную ломаную:
Таким образом, с каждым шагом общая длина линии возрастает на треть, т.е. в раза. Т.к. это число больше единицы, то получаемая геометрическая прогрессия с ростом числа шагом будет возрастать неограниченно.
раза. Т.к. это число больше единицы, то получаемая геометрическая прогрессия с ростом числа шагом будет возрастать неограниченно.
Длина кривой Коха бесконечна.
Таким образом, с каждым шагом общая длина линии возрастает на треть, т.е. в
Длина кривой Коха бесконечна.
понедельник, 11 октября 2010 г.
Генерация фрактальных деревьев
Вот такие двух-и трёхмерные фрактальные деревья может создавать программа, представленная в блоге Fractal World. Там вообще можно найти множество интересных алгебраических и геометрических фракталов с алгоритмами построения.
воскресенье, 10 октября 2010 г.
суббота, 9 октября 2010 г.
Иррациональный формат
Отношение сторон листа бумаги форматов А равно 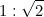 .
.
Листы меньшего формата получаются делением пополам листов большего. Отношение, таким образом, сохраняется:
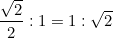
Листы меньшего формата получаются делением пополам листов большего. Отношение, таким образом, сохраняется:
вторник, 5 октября 2010 г.
понедельник, 4 октября 2010 г.
воскресенье, 3 октября 2010 г.
60
В Древнем Вавилоне использовали шестидесятеричную систему счисления. То есть узловыми были числа не 10, 100 и т.д., а 60, 3600 и т.д..
Одно из преимуществ шестидесятеричной системы в том, что многие периодичные в десятичной записи дроби будут там записываться конечной последовательностью цифр.
К примеру,
Отголоском этой системы является деление часа и градуса на 60 минут, а минуты - на 60 секунд.
Одно из преимуществ шестидесятеричной системы в том, что многие периодичные в десятичной записи дроби будут там записываться конечной последовательностью цифр.
К примеру,
Отголоском этой системы является деление часа и градуса на 60 минут, а минуты - на 60 секунд.
суббота, 2 октября 2010 г.
2+2=
В троичной системе всем известное равенство 2+2=4 выглядит как
2+2=11
Ведь 4=3+1 и записывается в троичной системе как число из двух единиц
четверг, 30 сентября 2010 г.
Двоичная система счисления
При записи чисел в десятичной системе счисления крайняя справа цифра означает количество единиц, следующая - десятков, далее - сотен, тысяч, десятков тысяч и т.д.
К примеру, 12365 = 5x100+6x101+3x102+2x103+1x104
Таким образом, для записи сколь угодно большого числа можно обойтись десятью разными цифрами. Но можно записывать любое число даже с помощью всего двух разных цифр: 0 и 1. Тогда цифры в соответствующих разрядах будут обозначать вхождение в число степеней двойки.
Число (1001011)2 = 1*20+1*21+0*22+1*23+0*24+0*25+1*26 = 1+2+8+64=(75)10
К примеру, 12365 = 5x100+6x101+3x102+2x103+1x104
Таким образом, для записи сколь угодно большого числа можно обойтись десятью разными цифрами. Но можно записывать любое число даже с помощью всего двух разных цифр: 0 и 1. Тогда цифры в соответствующих разрядах будут обозначать вхождение в число степеней двойки.
Число (1001011)2 = 1*20+1*21+0*22+1*23+0*24+0*25+1*26 = 1+2+8+64=(75)10
среда, 29 сентября 2010 г.
Принцип симметрии
Есть известная задача о стакане воды и бидоне молока. Из стакана воды ложку воды перелили в бидон молока, размешали, и затем перелили ложку смеси обратно в стакан воды. Чего больше: воды в молоке или молока в воде?
Задача, которую иногда пытаются решить с помощью сложных вычислений с дополнительными переменными, решается устно, если обратить внимание на простой факт. Т.к. объём, занятый в стакане воды, не изменился, то объём убывшей воды заменился объёмом прибывшего молока. Так что эти объёмы одинаковы, ведь вода из стакана убыла именно в бидон молока.
Задача, которую иногда пытаются решить с помощью сложных вычислений с дополнительными переменными, решается устно, если обратить внимание на простой факт. Т.к. объём, занятый в стакане воды, не изменился, то объём убывшей воды заменился объёмом прибывшего молока. Так что эти объёмы одинаковы, ведь вода из стакана убыла именно в бидон молока.
вторник, 28 сентября 2010 г.
Как превратить число в цепную дробь
Для этого нужно повторять действия взятия целой части числа и нахождения обратной величины от результата.
Пример: представить в виде цепной дроби число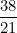
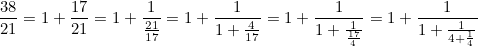
Таким образом, искомая цепная дробь имеет вид [1, 1, 4, 4]
Пример: представить в виде цепной дроби число
Таким образом, искомая цепная дробь имеет вид [1, 1, 4, 4]
понедельник, 27 сентября 2010 г.
Е в виде цепной дроби
Число е является трансцендентным, поэтому его цепная дробь непериодична. Но всё же явная закономерность в ней есть:
Удобнее записывать разложение числа в цепную дробь так:
e=[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, ...]
Удобнее записывать разложение числа в цепную дробь так:
e=[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, ...]
воскресенье, 26 сентября 2010 г.
Бесконечная цепная дробь
Число фи, коэффициент золотого сечения получается из бесконечной цепной дроби:
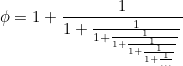
суббота, 25 сентября 2010 г.
Синус равен трём и в мирное время
Из экзаменационной работы:
Дано: x - острый угол,
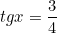 .
.
Найти его синус.
Решение
Т.к.
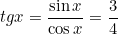
то sin x=3
Дано: x - острый угол,
Найти его синус.
Решение
Т.к.
то sin x=3
пятница, 24 сентября 2010 г.
Компьютеру виднее
Реальный случай. Учу своих курсантов вычислять в Экселе формулы. И вот попросил одного товарища вычислить синус тридцати градусов.
Формула =sin(30), введённая им в ячейку дала результат -0,988, который и был предъявлен мне
Решил проверить понимание. Интересуюсь:
- Вы тут ничего подозрительного не замечаете?
- Нет...
- Но помните, в школе вы учили таблицы значений синуса? Помните, что там синус тридцати был равен одной второй?
- Да, вроде бы...
- А почему тут получилось другое значение?
- Ну, это компьютер точнее считает.
Формула =sin(30), введённая им в ячейку дала результат -0,988, который и был предъявлен мне
Решил проверить понимание. Интересуюсь:
- Вы тут ничего подозрительного не замечаете?
- Нет...
- Но помните, в школе вы учили таблицы значений синуса? Помните, что там синус тридцати был равен одной второй?
- Да, вроде бы...
- А почему тут получилось другое значение?
- Ну, это компьютер точнее считает.
четверг, 23 сентября 2010 г.
2 - число составное
Да-да, на множестве целых комплексных чисел (вида a+bi, где a, b - целые, а i2=-1) число 2 раскладывается на множители как:
2=(1+i)(1-i)
среда, 22 сентября 2010 г.
Безумная гравитация
Как-то, моделируя гравитационное взаимодействие, я задумался: а что было бы, если на определённом расстоянии от тела притяжение сменялось отталкиванием? Как бы тогда выглядели траектории планет?
Как оказалось, они бы двигались по довольно замысловатым траекториям. Убедиться в этом можно, скачав соответствующую программу. Управление в ней простое: левый щелчок - добавить лёгкую планету, Ctrl+левая кнопка - добавить тяжёлую планету. Правая кнопка - очистить экран от следов планет.
Вокруг каждой планеты, чередуясь, идут по 4 зоны отталкивания и притяжения. В результате получается что-то вроде этого:
Скачать программу моделирования гравитации (150 кБ)
Как оказалось, они бы двигались по довольно замысловатым траекториям. Убедиться в этом можно, скачав соответствующую программу. Управление в ней простое: левый щелчок - добавить лёгкую планету, Ctrl+левая кнопка - добавить тяжёлую планету. Правая кнопка - очистить экран от следов планет.
Вокруг каждой планеты, чередуясь, идут по 4 зоны отталкивания и притяжения. В результате получается что-то вроде этого:
Скачать программу моделирования гравитации (150 кБ)
вторник, 21 сентября 2010 г.
Нарочно не придумаешь
Вот какую задачу предлагается решить одиннадцатиклассникам при изучении темы Интегралы:
"Скорость движения точки задана уравнением v=3cos t (м/с). Найти уравнение движения, если в начальный момент времени точка находилась на расстоянии 2 м от начального положения."
Понятно, что авторы имели в виду, что x0=2 (м), однако такая формулировка задачи заставляет представлять точку, которая в начале движения отстоит от самой себя на 2 метра! о_О Это уже квантовая механика получается - в ней, согласно принципу неопределённости, невозможно, однозначно определив импульс частицы, точно установить её координаты. :)
"Скорость движения точки задана уравнением v=3cos t (м/с). Найти уравнение движения, если в начальный момент времени точка находилась на расстоянии 2 м от начального положения."
Понятно, что авторы имели в виду, что x0=2 (м), однако такая формулировка задачи заставляет представлять точку, которая в начале движения отстоит от самой себя на 2 метра! о_О Это уже квантовая механика получается - в ней, согласно принципу неопределённости, невозможно, однозначно определив импульс частицы, точно установить её координаты. :)
понедельник, 20 сентября 2010 г.
3816547290
Это число интересно тем, что все его 10 цифр различны и
число, образованное его первой цифрой (3) делится на 1
число, образованное его первыми 2мя цифрами (38) делится на 2
число, образованное его первыми 3мя цифрами (381) делится на 3
число, образованное его первыми 4мя цифрами (3816) делится на 4
число, образованное его первыми 5ю цифрами (38165) делится на 5
число, образованное его первыми 6ю цифрами (381654) делится на 6
число, образованное его первыми 7ю цифрами (3816547) делится на 7
число, образованное его первыми 8ю цифрами (38165472) делится на 8
число, образованное его первыми 9ю цифрами (381654729) делится на 9
число, образованное его первыми 10ю цифрами (3816547290) делится на 10.
число, образованное его первой цифрой (3) делится на 1
число, образованное его первыми 2мя цифрами (38) делится на 2
число, образованное его первыми 3мя цифрами (381) делится на 3
число, образованное его первыми 4мя цифрами (3816) делится на 4
число, образованное его первыми 5ю цифрами (38165) делится на 5
число, образованное его первыми 6ю цифрами (381654) делится на 6
число, образованное его первыми 7ю цифрами (3816547) делится на 7
число, образованное его первыми 8ю цифрами (38165472) делится на 8
число, образованное его первыми 9ю цифрами (381654729) делится на 9
число, образованное его первыми 10ю цифрами (3816547290) делится на 10.
воскресенье, 19 сентября 2010 г.
суббота, 18 сентября 2010 г.
Приближение числа е
Вот такое приближение числа е, дающее 10 верных знаков нашёл в 1966 году Георгий с форума e-science.ru:
пятница, 17 сентября 2010 г.
0=1
По формуле интегрирования частями
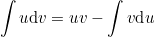 Применим её для вычисления интеграла
Применим её для вычисления интеграла
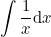 Подставим
Подставим
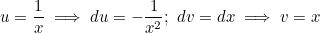 Тогда
Тогда
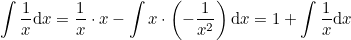 Таким образом,
Таким образом,
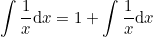 И, вычтя из левой и правой части равенства по исходном интегралу, получим:
И, вычтя из левой и правой части равенства по исходном интегралу, получим:
0=1
четверг, 16 сентября 2010 г.
среда, 15 сентября 2010 г.
вторник, 14 сентября 2010 г.
Возведение в квадрат числа, оканчивающегося на 5
Чтобы возвести в квадрат число, оканчивающееся пятёркой, нужно умножить число, полученное отбрасыванием последней пятёрки на следующее в натуральном ряду, и к результату приписать 25.
Примеры:
652
Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.
1152
Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.
Математическое обоснование:
Возведём в квадрат число 10n+5. (10n+5)2 = 100n2+100n+25 = 100n(n+1)+25, откуда и следует данное правило.
Примеры:
652
Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.
1152
Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.
Математическое обоснование:
Возведём в квадрат число 10n+5. (10n+5)2 = 100n2+100n+25 = 100n(n+1)+25, откуда и следует данное правило.
понедельник, 13 сентября 2010 г.
Ко Дню программиста :)
Взял и добавил несколько настроек к своей программе "Жизнь бактерий".
Можно регулировать:
Варьируя данные параметры, можно получать интересные результаты. К примеру, эта картинка:

Получена для 32 видов бактерий, окрестности Мура, и правила питания "n-я бактерия питается (n+2)й"
Скачать Lifecycle v.1.1. (165кБ)
Можно регулировать:
- Количество видов бактерий (Number of Species)
- Считаются ли клетки, соединённые по диагонали, соседями (если выбрать Neighborhood rule von Neumann, то не считаются, если Moore - то да).
- Правило, по которому для бактерии определяется вид, которым она питается (к примеру, Bacteria No n eats bacterii No n+2 означает, что 1й вид питается 3м, 2й - 4м и т.д.)
- Гарантированно ли охотник съедает свою добычу (чтобы дать добыче шанс установите Probability of eating менее 100).
Варьируя данные параметры, можно получать интересные результаты. К примеру, эта картинка:
Получена для 32 видов бактерий, окрестности Мура, и правила питания "n-я бактерия питается (n+2)й"
Скачать Lifecycle v.1.1. (165кБ)
воскресенье, 12 сентября 2010 г.
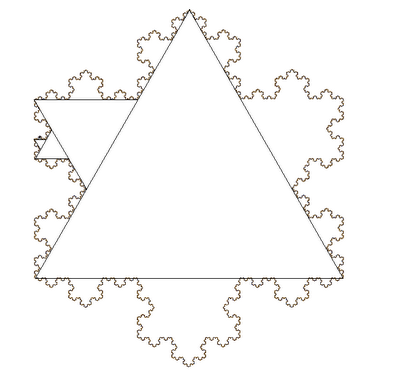
Кривая Коха
Давненько не было фракталов :)
Итак, Кривая Коха или Снежинка Коха строится так: В равностороннем треугольнике каждая сторона делится на три равные части, и на средних отрезках сторон строятся наружу равносторонние треугольники. Эту итерацию повторяют бесконечное число раз для каждого из отрезков ломаной, получившейся на предыдущем шаге.
На рисунке приведено несколько вспомогательных линий для иллюстрации способа построения.
Итак, Кривая Коха или Снежинка Коха строится так: В равностороннем треугольнике каждая сторона делится на три равные части, и на средних отрезках сторон строятся наружу равносторонние треугольники. Эту итерацию повторяют бесконечное число раз для каждого из отрезков ломаной, получившейся на предыдущем шаге.
На рисунке приведено несколько вспомогательных линий для иллюстрации способа построения.
суббота, 11 сентября 2010 г.
Принцип Дирихле
В городе с населением в 300 тысяч человек наверняка найдутся трое, у которых одинаковое количество волос на голове.
Действительно, ведь т.к. у человека на голове не более 140 тысяч волос, среди 140 001 человека обязаны найтись двое с одинаковым их количеством. А если рассмотреть группу, большую чем 280 тысяч, тот непременно найдутся уже трое.
Действительно, ведь т.к. у человека на голове не более 140 тысяч волос, среди 140 001 человека обязаны найтись двое с одинаковым их количеством. А если рассмотреть группу, большую чем 280 тысяч, тот непременно найдутся уже трое.
пятница, 10 сентября 2010 г.
Дни рождения
В классе из 22 человек вероятность того, что у двоих учеников дни рождения совпадают, более 50%.
четверг, 9 сентября 2010 г.
Гости и зонты
Есть такая задача:
В гости пришло n человек, т.к. в это время шёл дождь, все они были с зонтами. Расходились они в темноте, и каждый взял случайный зонт. Какова вероятность того, что ни один гость не ушёл со своим зонтом?
Для n=2 искомая вероятность , для троих гостей -
, для троих гостей -  , для четверых -
, для четверых -  , а с ростом n эта вероятность будет стремиться к
, а с ростом n эта вероятность будет стремиться к 
В гости пришло n человек, т.к. в это время шёл дождь, все они были с зонтами. Расходились они в темноте, и каждый взял случайный зонт. Какова вероятность того, что ни один гость не ушёл со своим зонтом?
Для n=2 искомая вероятность
Подписаться на:
Сообщения (Atom)
Популярные сообщения
-
Если вы хотите проверить, содержится ли ваш телефон, год рождения или номер дома среди уже вычисленных знаков числа пи, воспользуйтесь этой ...
-
Как рассказал наш читатель в комментарии к посту о целочисленном треугольнике , площадь четырёхугольника, вписанного в окружность, вычисляе...
-
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат...
-
Приведённые квадратные уравнения легко решать по теореме Виета. Достаточно найти два числа такие, произведение которых равно свободному член...
-
Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существуе...
-
Ещё одна задачка про матрицы. Рассмотрим матрицы 3х3, элементами которых могут быть только нули, единицы и двойки. Всего таким матриц будет ...
-
Самый длинный месяц у нас - это октябрь.Из-за перевода часов он на час длиннее остальных месяцев, в которых по 31 дню.
-
Для числа 12 на математических часах я выбрал одну их наиболее парадоксальных формул, согласно которой сумма всего бесконечного множества на...
-
Факториал числа n выражает количество способов расставить n разных предметов в ряд. Если же требуется расставить эти же n предметов в ряд, ...
-
Давайте начнём новый, 2022й год с интересной задачи. Рассмотрим квадратную таблицу. Попробуем её заполнить натуральными числами так, чтобы с...
Темы
число
цифра
простые
геометрия
юмор
дроби
язык
степень
делимость
пи
методы
история
квадрат
самоописывающее
время
задача
система счисления
узор
корень
тригонометрия
структура
е
сайты
конструкция
формулы
игра
факториал
функции
приближение
программа
фрактал
комбинаторика
последовательность
график
память
логарифм
вероятность
палиндром
пределы
конкурс
треугольник
магический квадрат
неизвестное
правильно-неправильное действие
видео
интеграл
уравнение
комплексные
софизм
заблуждения
процесс
ряды
цитаты
книги
окружность
прогрессия
среднее
стереометрия
число фи
выражения
графы
матрица
проценты
разрезания
логика
парабола
символ
статистика
2014
Фибоначчи
клеточный автомат
кривая
производная
фокус
головоломка
действия
иллюзия
куб
шахматы
многоугольник
новости
оказывается
оригами
подобие
построение
сложение
термин
тетраэдр
топология