Метод решения квадратных уравнений с помощью дискриминанта знают почти все. Но, как мне пришлось убедиться, для многих эта формула: D = b2 - 4ac кажется своего рода заклинанием. И почему для получения корней сначала нужно произвести именно такую операцию с коэффициентами - загадка.
Чтобы понять, откуда взялась формула дискриминанта и почему она работает, попробуем решить квадратное уравнение без неё.
Итак, имеем уравнение ax2 + bx + c = 0, где первый коэффициент не равен нулю.
Для начала разделим обе части на a:
Было б здорово, если бы левую часть удалось свернуть по формуле квадрата суммы. Квадрат первого, x2 , уже есть. Тогда удвоенным произведением первого на второе должно стать: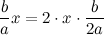
Квадрат второго будет равняться
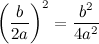
Прибавим его и отнимем от левой части уравнения:
Соберём три слагаемых левой части в квадрат суммы, а оставшиеся два - перенесём вправо:
Приведём правую часть к общему знаменателю:
Вот он! Выражение b2 - 4ac, стоящее в числителе правой части - и есть наш дискриминант. Почему же его знак определяет количество корней? Рассмотрим полученное уравнение внимательнее. Слева стоит квадрат. В знаменателе правой части - тоже квадрат. И только дискриминант может иметь любой знак. Поэтому, если он окажется отрицательным, полученное уравнение корней иметь не будет. Если нулевым - корень будет единственным (кстати, формула нахождения вершины параболы также происходит отсюда). И только для положительного дискриминанта будет 2 различных корня.
Ну а дальше - легко :)
Чтобы понять, откуда взялась формула дискриминанта и почему она работает, попробуем решить квадратное уравнение без неё.
Итак, имеем уравнение ax2 + bx + c = 0, где первый коэффициент не равен нулю.
Для начала разделим обе части на a:
Было б здорово, если бы левую часть удалось свернуть по формуле квадрата суммы. Квадрат первого, x2 , уже есть. Тогда удвоенным произведением первого на второе должно стать:
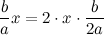
Квадрат второго будет равняться
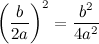
Прибавим его и отнимем от левой части уравнения:
Вот он! Выражение b2 - 4ac, стоящее в числителе правой части - и есть наш дискриминант. Почему же его знак определяет количество корней? Рассмотрим полученное уравнение внимательнее. Слева стоит квадрат. В знаменателе правой части - тоже квадрат. И только дискриминант может иметь любой знак. Поэтому, если он окажется отрицательным, полученное уравнение корней иметь не будет. Если нулевым - корень будет единственным (кстати, формула нахождения вершины параболы также происходит отсюда). И только для положительного дискриминанта будет 2 различных корня.
Ну а дальше - легко :)
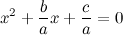
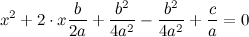
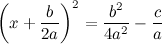
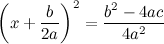



Для некоторых студентов ещё большим заклинанием является формула: d(ln(x))/dx = 1/x, в то время как для других логарифмов там ещё множитель :) Хотя доказывается тоже легко.
ОтветитьУдалитьдля меня сама буква d -заклинание
Удалить