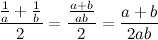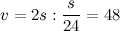Классическая задача, в которой автобус едет из пункта А в пункт В со скоростью 40к/ч, а возвращается со скоростью 60 км/ч, часто направляет по ложному следу школьника, которому необходимо найти среднюю скорость.
Очевидный шаг - найти среднее арифметическое скоростей "туда" и "обратно", дающий ответ 50 км/ч, является неправильным. И вот почему: двигаясь с меньшей скоростью, автобус затратит большее время на путь, следовательно, эта скорость окажет большее влияние на среднюю. Рассмотрим крайний случай: скорость "туда" равна 100 км/ч, а обратно - 0 км/ч. Среднее арифметическое этих скоростей, опять-таки, 50 км/ч, но в данном случае автобус и вовсе не прибудет в пункт А.
Чтобы правильно решать подобные задачи, необходимо вспомнить определение средней скорости. Средняя скорость является отношением всего пройденного расстояния к общему затраченному времени.
Пусть расстояние между пунктами равно s. Тогда автобус прошёл расстояние, равное 2s. Времени на путь из А в В он затратил s/40 ч, а на обратный - s/60 ч. Общее время составит:
Теперь можно находить среднюю скорость.


.PNG/224px-Pythagorean_graphic_(2).PNG)

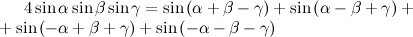


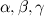
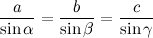

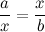
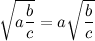


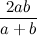 , по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.
, по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.