При записи чисел в десятичной системе счисления крайняя справа цифра означает количество единиц, следующая - десятков, далее - сотен, тысяч, десятков тысяч и т.д.
К примеру, 12365 = 5x100+6x101+3x102+2x103+1x104
Таким образом, для записи сколь угодно большого числа можно обойтись десятью разными цифрами. Но можно записывать любое число даже с помощью всего двух разных цифр: 0 и 1. Тогда цифры в соответствующих разрядах будут обозначать вхождение в число степеней двойки.
Число (1001011)2 = 1*20+1*21+0*22+1*23+0*24+0*25+1*26 = 1+2+8+64=(75)10
Интересные числа, занимательные математические факты и удивительные конструкции. Узнавайте каждый день что-то новое!
четверг, 30 сентября 2010 г.
среда, 29 сентября 2010 г.
Принцип симметрии
Есть известная задача о стакане воды и бидоне молока. Из стакана воды ложку воды перелили в бидон молока, размешали, и затем перелили ложку смеси обратно в стакан воды. Чего больше: воды в молоке или молока в воде?
Задача, которую иногда пытаются решить с помощью сложных вычислений с дополнительными переменными, решается устно, если обратить внимание на простой факт. Т.к. объём, занятый в стакане воды, не изменился, то объём убывшей воды заменился объёмом прибывшего молока. Так что эти объёмы одинаковы, ведь вода из стакана убыла именно в бидон молока.
Задача, которую иногда пытаются решить с помощью сложных вычислений с дополнительными переменными, решается устно, если обратить внимание на простой факт. Т.к. объём, занятый в стакане воды, не изменился, то объём убывшей воды заменился объёмом прибывшего молока. Так что эти объёмы одинаковы, ведь вода из стакана убыла именно в бидон молока.
вторник, 28 сентября 2010 г.
Как превратить число в цепную дробь
Для этого нужно повторять действия взятия целой части числа и нахождения обратной величины от результата.
Пример: представить в виде цепной дроби число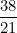
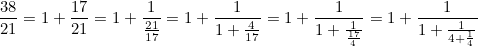
Таким образом, искомая цепная дробь имеет вид [1, 1, 4, 4]
Пример: представить в виде цепной дроби число
Таким образом, искомая цепная дробь имеет вид [1, 1, 4, 4]
понедельник, 27 сентября 2010 г.
Е в виде цепной дроби
Число е является трансцендентным, поэтому его цепная дробь непериодична. Но всё же явная закономерность в ней есть:
Удобнее записывать разложение числа в цепную дробь так:
e=[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, ...]
Удобнее записывать разложение числа в цепную дробь так:
e=[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, ...]
воскресенье, 26 сентября 2010 г.
Бесконечная цепная дробь
Число фи, коэффициент золотого сечения получается из бесконечной цепной дроби:
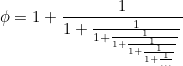
суббота, 25 сентября 2010 г.
Синус равен трём и в мирное время
Из экзаменационной работы:
Дано: x - острый угол,
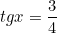 .
.
Найти его синус.
Решение
Т.к.
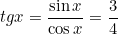
то sin x=3
Дано: x - острый угол,
Найти его синус.
Решение
Т.к.
то sin x=3
пятница, 24 сентября 2010 г.
Компьютеру виднее
Реальный случай. Учу своих курсантов вычислять в Экселе формулы. И вот попросил одного товарища вычислить синус тридцати градусов.
Формула =sin(30), введённая им в ячейку дала результат -0,988, который и был предъявлен мне
Решил проверить понимание. Интересуюсь:
- Вы тут ничего подозрительного не замечаете?
- Нет...
- Но помните, в школе вы учили таблицы значений синуса? Помните, что там синус тридцати был равен одной второй?
- Да, вроде бы...
- А почему тут получилось другое значение?
- Ну, это компьютер точнее считает.
Формула =sin(30), введённая им в ячейку дала результат -0,988, который и был предъявлен мне
Решил проверить понимание. Интересуюсь:
- Вы тут ничего подозрительного не замечаете?
- Нет...
- Но помните, в школе вы учили таблицы значений синуса? Помните, что там синус тридцати был равен одной второй?
- Да, вроде бы...
- А почему тут получилось другое значение?
- Ну, это компьютер точнее считает.
четверг, 23 сентября 2010 г.
2 - число составное
Да-да, на множестве целых комплексных чисел (вида a+bi, где a, b - целые, а i2=-1) число 2 раскладывается на множители как:
2=(1+i)(1-i)
среда, 22 сентября 2010 г.
Безумная гравитация
Как-то, моделируя гравитационное взаимодействие, я задумался: а что было бы, если на определённом расстоянии от тела притяжение сменялось отталкиванием? Как бы тогда выглядели траектории планет?
Как оказалось, они бы двигались по довольно замысловатым траекториям. Убедиться в этом можно, скачав соответствующую программу. Управление в ней простое: левый щелчок - добавить лёгкую планету, Ctrl+левая кнопка - добавить тяжёлую планету. Правая кнопка - очистить экран от следов планет.
Вокруг каждой планеты, чередуясь, идут по 4 зоны отталкивания и притяжения. В результате получается что-то вроде этого:
Скачать программу моделирования гравитации (150 кБ)
Как оказалось, они бы двигались по довольно замысловатым траекториям. Убедиться в этом можно, скачав соответствующую программу. Управление в ней простое: левый щелчок - добавить лёгкую планету, Ctrl+левая кнопка - добавить тяжёлую планету. Правая кнопка - очистить экран от следов планет.
Вокруг каждой планеты, чередуясь, идут по 4 зоны отталкивания и притяжения. В результате получается что-то вроде этого:
Скачать программу моделирования гравитации (150 кБ)
вторник, 21 сентября 2010 г.
Нарочно не придумаешь
Вот какую задачу предлагается решить одиннадцатиклассникам при изучении темы Интегралы:
"Скорость движения точки задана уравнением v=3cos t (м/с). Найти уравнение движения, если в начальный момент времени точка находилась на расстоянии 2 м от начального положения."
Понятно, что авторы имели в виду, что x0=2 (м), однако такая формулировка задачи заставляет представлять точку, которая в начале движения отстоит от самой себя на 2 метра! о_О Это уже квантовая механика получается - в ней, согласно принципу неопределённости, невозможно, однозначно определив импульс частицы, точно установить её координаты. :)
"Скорость движения точки задана уравнением v=3cos t (м/с). Найти уравнение движения, если в начальный момент времени точка находилась на расстоянии 2 м от начального положения."
Понятно, что авторы имели в виду, что x0=2 (м), однако такая формулировка задачи заставляет представлять точку, которая в начале движения отстоит от самой себя на 2 метра! о_О Это уже квантовая механика получается - в ней, согласно принципу неопределённости, невозможно, однозначно определив импульс частицы, точно установить её координаты. :)
понедельник, 20 сентября 2010 г.
3816547290
Это число интересно тем, что все его 10 цифр различны и
число, образованное его первой цифрой (3) делится на 1
число, образованное его первыми 2мя цифрами (38) делится на 2
число, образованное его первыми 3мя цифрами (381) делится на 3
число, образованное его первыми 4мя цифрами (3816) делится на 4
число, образованное его первыми 5ю цифрами (38165) делится на 5
число, образованное его первыми 6ю цифрами (381654) делится на 6
число, образованное его первыми 7ю цифрами (3816547) делится на 7
число, образованное его первыми 8ю цифрами (38165472) делится на 8
число, образованное его первыми 9ю цифрами (381654729) делится на 9
число, образованное его первыми 10ю цифрами (3816547290) делится на 10.
число, образованное его первой цифрой (3) делится на 1
число, образованное его первыми 2мя цифрами (38) делится на 2
число, образованное его первыми 3мя цифрами (381) делится на 3
число, образованное его первыми 4мя цифрами (3816) делится на 4
число, образованное его первыми 5ю цифрами (38165) делится на 5
число, образованное его первыми 6ю цифрами (381654) делится на 6
число, образованное его первыми 7ю цифрами (3816547) делится на 7
число, образованное его первыми 8ю цифрами (38165472) делится на 8
число, образованное его первыми 9ю цифрами (381654729) делится на 9
число, образованное его первыми 10ю цифрами (3816547290) делится на 10.
воскресенье, 19 сентября 2010 г.
суббота, 18 сентября 2010 г.
Приближение числа е
Вот такое приближение числа е, дающее 10 верных знаков нашёл в 1966 году Георгий с форума e-science.ru:
пятница, 17 сентября 2010 г.
0=1
По формуле интегрирования частями
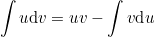 Применим её для вычисления интеграла
Применим её для вычисления интеграла
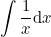 Подставим
Подставим
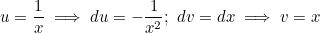 Тогда
Тогда
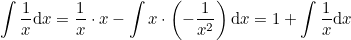 Таким образом,
Таким образом,
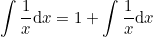 И, вычтя из левой и правой части равенства по исходном интегралу, получим:
И, вычтя из левой и правой части равенства по исходном интегралу, получим:
0=1
четверг, 16 сентября 2010 г.
среда, 15 сентября 2010 г.
вторник, 14 сентября 2010 г.
Возведение в квадрат числа, оканчивающегося на 5
Чтобы возвести в квадрат число, оканчивающееся пятёркой, нужно умножить число, полученное отбрасыванием последней пятёрки на следующее в натуральном ряду, и к результату приписать 25.
Примеры:
652
Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.
1152
Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.
Математическое обоснование:
Возведём в квадрат число 10n+5. (10n+5)2 = 100n2+100n+25 = 100n(n+1)+25, откуда и следует данное правило.
Примеры:
652
Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.
1152
Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.
Математическое обоснование:
Возведём в квадрат число 10n+5. (10n+5)2 = 100n2+100n+25 = 100n(n+1)+25, откуда и следует данное правило.
понедельник, 13 сентября 2010 г.
Ко Дню программиста :)
Взял и добавил несколько настроек к своей программе "Жизнь бактерий".
Можно регулировать:
Варьируя данные параметры, можно получать интересные результаты. К примеру, эта картинка:

Получена для 32 видов бактерий, окрестности Мура, и правила питания "n-я бактерия питается (n+2)й"
Скачать Lifecycle v.1.1. (165кБ)
Можно регулировать:
- Количество видов бактерий (Number of Species)
- Считаются ли клетки, соединённые по диагонали, соседями (если выбрать Neighborhood rule von Neumann, то не считаются, если Moore - то да).
- Правило, по которому для бактерии определяется вид, которым она питается (к примеру, Bacteria No n eats bacterii No n+2 означает, что 1й вид питается 3м, 2й - 4м и т.д.)
- Гарантированно ли охотник съедает свою добычу (чтобы дать добыче шанс установите Probability of eating менее 100).
Варьируя данные параметры, можно получать интересные результаты. К примеру, эта картинка:
Получена для 32 видов бактерий, окрестности Мура, и правила питания "n-я бактерия питается (n+2)й"
Скачать Lifecycle v.1.1. (165кБ)
воскресенье, 12 сентября 2010 г.
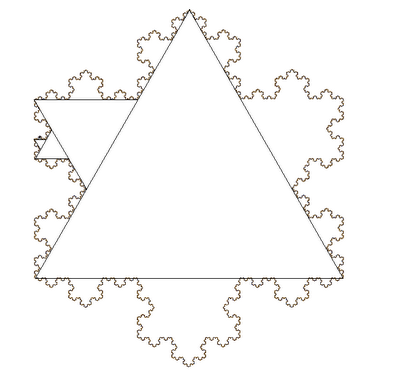
Кривая Коха
Давненько не было фракталов :)
Итак, Кривая Коха или Снежинка Коха строится так: В равностороннем треугольнике каждая сторона делится на три равные части, и на средних отрезках сторон строятся наружу равносторонние треугольники. Эту итерацию повторяют бесконечное число раз для каждого из отрезков ломаной, получившейся на предыдущем шаге.
На рисунке приведено несколько вспомогательных линий для иллюстрации способа построения.
Итак, Кривая Коха или Снежинка Коха строится так: В равностороннем треугольнике каждая сторона делится на три равные части, и на средних отрезках сторон строятся наружу равносторонние треугольники. Эту итерацию повторяют бесконечное число раз для каждого из отрезков ломаной, получившейся на предыдущем шаге.
На рисунке приведено несколько вспомогательных линий для иллюстрации способа построения.
суббота, 11 сентября 2010 г.
Принцип Дирихле
В городе с населением в 300 тысяч человек наверняка найдутся трое, у которых одинаковое количество волос на голове.
Действительно, ведь т.к. у человека на голове не более 140 тысяч волос, среди 140 001 человека обязаны найтись двое с одинаковым их количеством. А если рассмотреть группу, большую чем 280 тысяч, тот непременно найдутся уже трое.
Действительно, ведь т.к. у человека на голове не более 140 тысяч волос, среди 140 001 человека обязаны найтись двое с одинаковым их количеством. А если рассмотреть группу, большую чем 280 тысяч, тот непременно найдутся уже трое.
пятница, 10 сентября 2010 г.
Дни рождения
В классе из 22 человек вероятность того, что у двоих учеников дни рождения совпадают, более 50%.
четверг, 9 сентября 2010 г.
Гости и зонты
Есть такая задача:
В гости пришло n человек, т.к. в это время шёл дождь, все они были с зонтами. Расходились они в темноте, и каждый взял случайный зонт. Какова вероятность того, что ни один гость не ушёл со своим зонтом?
Для n=2 искомая вероятность , для троих гостей -
, для троих гостей -  , для четверых -
, для четверых -  , а с ростом n эта вероятность будет стремиться к
, а с ростом n эта вероятность будет стремиться к 
В гости пришло n человек, т.к. в это время шёл дождь, все они были с зонтами. Расходились они в темноте, и каждый взял случайный зонт. Какова вероятность того, что ни один гость не ушёл со своим зонтом?
Для n=2 искомая вероятность
среда, 8 сентября 2010 г.
Мгновение арифметической прогрессии
Сегодня, пока большинство из нас досматривали предрассветные сны, наступила удивительная секунда.
А именно: 5 часов утра, 6 минут и 7 секунд 8 числа 9 месяца 10 года.
А именно: 5 часов утра, 6 минут и 7 секунд 8 числа 9 месяца 10 года.
вторник, 7 сентября 2010 г.
Как запомнить число e
Способ помнить е простой - два, семь, дважды Лев Толстой.
Дело в том, что 1828 - год рождения Льва Николаевича Толстого.
e=2,718281828...
В связи с этим есть шутка.
Люди делятся на 3 категории:
Те, кто запоминает число е через год рождения Льва Толстого,
Те, кто запоминает год рождения Льва Толстого через число е (к этой отношусь я :) ),
И те, кому наплевать, и на число е, и на Льва Толстого.
Дело в том, что 1828 - год рождения Льва Николаевича Толстого.
e=2,718281828...
В связи с этим есть шутка.
Люди делятся на 3 категории:
Те, кто запоминает число е через год рождения Льва Толстого,
Те, кто запоминает год рождения Льва Толстого через число е (к этой отношусь я :) ),
И те, кому наплевать, и на число е, и на Льва Толстого.
понедельник, 6 сентября 2010 г.
Второй замечательный предел.
Допустим, мы кладём 1 доллар на счёт под 100% годовых с выплатой процентов в конце срока. Через год у нас будет 2 доллара.
А что если на вклад будет начисляться по 50% каждые 6 месяцев? Тогда черед полгода у нас будет 1,5 доллара, а через год 1,5x1,5=2,25 доллара, что больше двух долларов.
А если каждый квартал вклад будет увеличиваться на 25%?
В конце первого квартала на счету будет 1,25 доллара. Через полгода 1,251,5625. Через девять месяцев - 1,5625x1,25=1,953125. А через год начислится 1,953125x1,25=2,44140625 - ещё больше, чем в предыдущем случае.
Будет ли получаемая сумма расти неограниченно с уменьшением сроков выплат процентов? Посмотрим, что будет с ежедневным начислением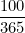 процента. По аналогии с предыдущими вычислениями можно получить, что сумма на счету составит
процента. По аналогии с предыдущими вычислениями можно получить, что сумма на счету составит 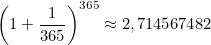
Рост по сравнению с ежеквартальным начислением незначительный.
Так вот, оказывается, что если продолжать уменьшать сроки между выплатами практически до нуля, вклад в конечном счёте увеличится в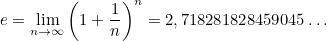 раз.
раз.
Число е играет важную роль в математике, в частности, в описании процессов, связанных с ростом.
А что если на вклад будет начисляться по 50% каждые 6 месяцев? Тогда черед полгода у нас будет 1,5 доллара, а через год 1,5x1,5=2,25 доллара, что больше двух долларов.
А если каждый квартал вклад будет увеличиваться на 25%?
В конце первого квартала на счету будет 1,25 доллара. Через полгода 1,251,5625. Через девять месяцев - 1,5625x1,25=1,953125. А через год начислится 1,953125x1,25=2,44140625 - ещё больше, чем в предыдущем случае.
Будет ли получаемая сумма расти неограниченно с уменьшением сроков выплат процентов? Посмотрим, что будет с ежедневным начислением
Рост по сравнению с ежеквартальным начислением незначительный.
Так вот, оказывается, что если продолжать уменьшать сроки между выплатами практически до нуля, вклад в конечном счёте увеличится в
Число е играет важную роль в математике, в частности, в описании процессов, связанных с ростом.
воскресенье, 5 сентября 2010 г.
Почему же гиперболические?
Почему же функции sh, ch, th называются гиперболическими синусом, косинусом и тангенсом?
Вспомним, как определяются значения тригонометрических функций для произвольного t.
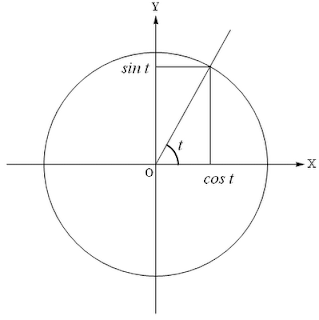
Если на единичной окружности, задаваемой уравнением x2+y2=1, отложить от оси ОХ против часовой стрелки угол t, то синусом его будет проекция соответствующей точки окружности на ось у, а косинусом - на ось х.
Заметим также, что угол t численно равен площади S вырезаемого им сектора окружности (примем, что при каждом переходе через полный круг, площадь всё увеличивается).
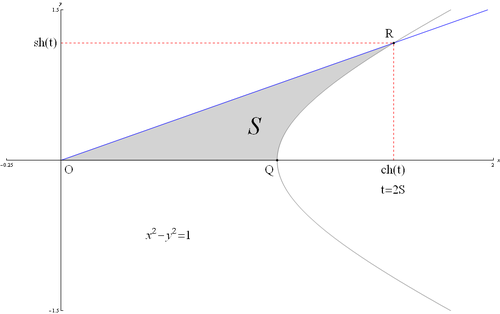
Гиперболические функции определяются аналогичным образом через гиперболу x2-y2=1 (как я рассказывал, гипербола - это не только график обратной пропорциональности)
Гиперболические синус и косинус будут проекциями точки пересечения луча, пущенного из начала координат с этой гиперболой на оси у и х, соответственно. Параметром t соответствующих функций берётся удвоенная площады S, заключённая между лучом, гиперболой и осью ОХ (если луч откладывается в нижнюю полуплоскость, берётся знак минус).
Вспомним, как определяются значения тригонометрических функций для произвольного t.

Если на единичной окружности, задаваемой уравнением x2+y2=1, отложить от оси ОХ против часовой стрелки угол t, то синусом его будет проекция соответствующей точки окружности на ось у, а косинусом - на ось х.
Заметим также, что угол t численно равен площади S вырезаемого им сектора окружности (примем, что при каждом переходе через полный круг, площадь всё увеличивается).
Гиперболические функции определяются аналогичным образом через гиперболу x2-y2=1 (как я рассказывал, гипербола - это не только график обратной пропорциональности)
Гиперболические синус и косинус будут проекциями точки пересечения луча, пущенного из начала координат с этой гиперболой на оси у и х, соответственно. Параметром t соответствующих функций берётся удвоенная площады S, заключённая между лучом, гиперболой и осью ОХ (если луч откладывается в нижнюю полуплоскость, берётся знак минус).
суббота, 4 сентября 2010 г.
Настраиваемый геймплей в CardWars
По итогам обсуждения своей игры на форумах, подготовил релиз для экспериментов с управлением и геймплеем. Можно регулировать механику игры в области сражений, раздачи карт, видимости карт противника и управления выбором опций Меню.
Скачать CardWars Flexible Gameplay Edition
Можно скачать только файл CardWarsFGE.exe (1 Мб) и поместить его в вашу папку с CardWars 0.5.2
Или, если вы версию 0.5.2 не скачивали, скачать полный архив (1,8 Мб)
Можно скачать только файл CardWarsFGE.exe (1 Мб) и поместить его в вашу папку с CardWars 0.5.2
Или, если вы версию 0.5.2 не скачивали, скачать полный архив (1,8 Мб)
Регулируются следующие параметры:
- Будет ли гарнизон, потерявший 50% карт, отступать, или сражаться до конца
- Будут ли провинции терять ход после атаки/захвата/прихода подкреплений
- Будут ли несколько одинаковых карт в колоде усиливать друг друга в битве
- Меру случайности в раздаче карт
- Будет ли игрок получать по 1 карте за каждую контролируемую провинцию, или только за те, которые на этом ходу не участвовали в битве
- Будет ли игрок видеть все карты противника, только верхнюю в каждой колоде или вообще лишь количество карт.
Также можно включить другой режим управления, в котором все действия выполняются левой кнопкой мыши, а правая служит для входа в окно сортировки карт.
Пожалуйста, попробуйте разные режимы и укажите, какие режимы игры понравились больше.
пятница, 3 сентября 2010 г.
Гиперболический тангенс
По аналогии c тригонометрическим, гиперболический тангенс - частное гиперболических синуса и косинуса.
График его имеет две горизонтальные асимптоты: y=1 в положительном направлении и y=-1 - в отрицательном.
Благодаря тому, что вблизи нуля функция изменяется быстро, а вдали от него - всё медленнее, гиперболический тангенс, наряду с другими функциями с таким свойством, используется при моделировании нейронных сетей.
График его имеет две горизонтальные асимптоты: y=1 в положительном направлении и y=-1 - в отрицательном.
Благодаря тому, что вблизи нуля функция изменяется быстро, а вдали от него - всё медленнее, гиперболический тангенс, наряду с другими функциями с таким свойством, используется при моделировании нейронных сетей.
четверг, 2 сентября 2010 г.
Гиперболический синус
Гиперболическим синусом называется функция
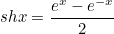
Разность квадратов гиперболических косинуса и синуса равна единице, так же как и сумма квадратов синуса и косинуса тригонометрических.
Разность квадратов гиперболических косинуса и синуса равна единице, так же как и сумма квадратов синуса и косинуса тригонометрических.
среда, 1 сентября 2010 г.
Как опубликовать математическую статью
Поздравляю с началом учебного года! Начнём его с математического юмора.
Допустим, вы хотите опубликовать что-то вроде
Таким образом, исходное уравнение может быть представлено в более "научном" виде как
что намного более внушительно. Однако не стоит останавливаться на достигнутом. Выражение можно усложнить далее, используя
Его можно спокойно публиковать в серьёзном журнале.
Примечание: Поняв основной принцип, можете использовать и другие преобразования для поднятия своего престижа.
Допустим, вы хотите опубликовать что-то вроде
1+1=2
Для научной статьи это не очень впечатляюще. Поэтому усложните левую часть, используя:1=ln(e) и 1=sin2x+cos2x
А правая часть может быть превращена вТаким образом, исходное уравнение может быть представлено в более "научном" виде как
что намного более внушительно. Однако не стоит останавливаться на достигнутом. Выражение можно усложнить далее, используя
Таким образом, исходное выражение может быть записано как:
Его можно спокойно публиковать в серьёзном журнале.
Примечание: Поняв основной принцип, можете использовать и другие преобразования для поднятия своего престижа.
Подписаться на:
Сообщения (Atom)
Популярные сообщения
-
Если вы хотите проверить, содержится ли ваш телефон, год рождения или номер дома среди уже вычисленных знаков числа пи, воспользуйтесь этой ...
-
Как рассказал наш читатель в комментарии к посту о целочисленном треугольнике , площадь четырёхугольника, вписанного в окружность, вычисляе...
-
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат...
-
Приведённые квадратные уравнения легко решать по теореме Виета. Достаточно найти два числа такие, произведение которых равно свободному член...
-
Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существуе...
-
Самый длинный месяц у нас - это октябрь.Из-за перевода часов он на час длиннее остальных месяцев, в которых по 31 дню.
-
Ещё одна задачка про матрицы. Рассмотрим матрицы 3х3, элементами которых могут быть только нули, единицы и двойки. Всего таким матриц будет ...
-
Для числа 12 на математических часах я выбрал одну их наиболее парадоксальных формул, согласно которой сумма всего бесконечного множества на...
-
Факториал числа n выражает количество способов расставить n разных предметов в ряд. Если же требуется расставить эти же n предметов в ряд, ...
-
Давайте начнём новый, 2022й год с интересной задачи. Рассмотрим квадратную таблицу. Попробуем её заполнить натуральными числами так, чтобы с...
Темы
число
цифра
простые
геометрия
юмор
дроби
язык
степень
делимость
пи
методы
история
квадрат
самоописывающее
время
задача
система счисления
узор
корень
тригонометрия
структура
е
сайты
конструкция
формулы
игра
факториал
функции
приближение
программа
фрактал
комбинаторика
последовательность
график
память
логарифм
вероятность
палиндром
пределы
конкурс
треугольник
магический квадрат
неизвестное
правильно-неправильное действие
видео
интеграл
уравнение
комплексные
софизм
заблуждения
процесс
ряды
цитаты
книги
окружность
прогрессия
среднее
стереометрия
число фи
выражения
графы
матрица
проценты
разрезания
логика
парабола
символ
статистика
2014
Фибоначчи
клеточный автомат
кривая
производная
фокус
головоломка
действия
иллюзия
куб
шахматы
многоугольник
новости
оказывается
оригами
подобие
построение
сложение
термин
тетраэдр
топология