Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существует способ получения цепной дроби любой длины, требующий лишь ручки и бумаги.
Разложим с его помощью корень из 503, который нам был нужен для решения уравнения Пелля.
Для начала выделим в корне целую часть. Так как 222 = 484, а 232 = 529, то
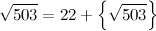
Итак, искомое разложение начнётся как [22, ....]
Превратим дробную часть в дробь с числителем 1:
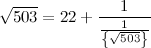
Избавимся от иррациональности в знаменателе дроби, воспользовавшись тем, что:
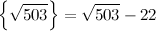
Получим:
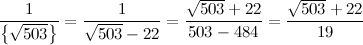
Теперь выделим у дроби целую часть:
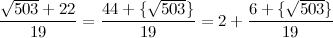
Получили второй член разложения: [22, 2, ....] А в целом цепная дробь сейчас выглядит так:
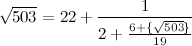
Перевернём теперь дробную часть ещё раз:
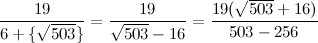
Внимание! Здесь начинается особая математическая магия! Дело в том, что знаменатель обязательно должен разделиться на целый множитель числителя. Очень рекомендую это доказать - удовольствие гарантировано.
Действительно, здесь тоже имеем:
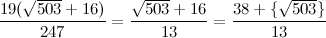
И выделение целой части даёт нам новый член разложения: [22, 2, 2, ....]
Вот новое звено цепной дроби:
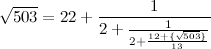
Данный процесс можно продолжать. Когда получим на каком-либо шаге дробь, которая получалась ранее (а мы обязательно получим такую, это тоже можно доказать), соответствующий участок разложения зациклится.
Вот так можно получить цепную дробь любого корня без каких-либо электронных вычислительных средств. А вообще, самый простой способ - это вбить в ВольфрамАльфе: continued fraction, а затем в новом открывшемся окошке написать sqrt(503)
Для начала выделим в корне целую часть. Так как 222 = 484, а 232 = 529, то
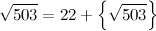
Итак, искомое разложение начнётся как [22, ....]
Превратим дробную часть в дробь с числителем 1:
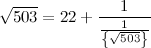
Избавимся от иррациональности в знаменателе дроби, воспользовавшись тем, что:
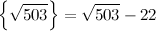
Получим:
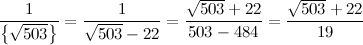
Теперь выделим у дроби целую часть:
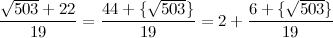
Получили второй член разложения: [22, 2, ....] А в целом цепная дробь сейчас выглядит так:
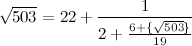
Перевернём теперь дробную часть ещё раз:
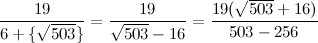
Внимание! Здесь начинается особая математическая магия! Дело в том, что знаменатель обязательно должен разделиться на целый множитель числителя. Очень рекомендую это доказать - удовольствие гарантировано.
Действительно, здесь тоже имеем:
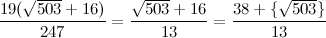
И выделение целой части даёт нам новый член разложения: [22, 2, 2, ....]
Вот новое звено цепной дроби:
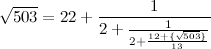
Данный процесс можно продолжать. Когда получим на каком-либо шаге дробь, которая получалась ранее (а мы обязательно получим такую, это тоже можно доказать), соответствующий участок разложения зациклится.
Вот так можно получить цепную дробь любого корня без каких-либо электронных вычислительных средств. А вообще, самый простой способ - это вбить в ВольфрамАльфе: continued fraction, а затем в новом открывшемся окошке написать sqrt(503)




Товарищ, я пытаюсь применить этот способ для числа 991, но ничего не выходит. На втором шагу было обещано, что разделится нацело, но у меня получается (30*(√991+30)/(991-900)=(30*(√991+30)/61). Более того, в Вольфраме второй член последовательности это 2, а у меня почему-то 1:
ОтветитьУдалить√991=31+1/1/{√991};
1/{√991}=(√991+31)/(991-961)=(√991+31)/30=1+(1+{√991})/30.
Прошу помощи ;) (x^2-991y^2=1 мое уравнение Петля)
Ах да, ещё такая проблема: в Вольфраме не получается период этой дроби (или я невнимательная).
Вы невнимательная, целая часть корня из 991 будет 31, как вам Вольфрам верно и написал.
ОтветитьУдалить