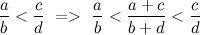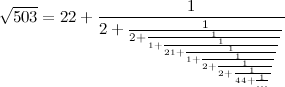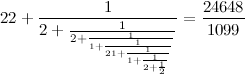Дружественные дроби

 Про дружественные числа и про их расширение - компанейские числа мы писали давно. А вчера в твиттере Клиффа Пиковера попалась заметка о дружественных дробях. В отличие от дружественных чисел, это понятние не универсально, а привязано к системе счисления, однако, посмотрите, как красиво:

Берём число 819

Дробь 1/819 выглядит в виде бесконечной периодической десятичной дроби как

1/819 = 0,001221001221001221001221001221...

А если посмотреть на дробь 1/1221, то получим:

 1/1221 = 0,000819000819000819000819000819...

 

Найдутся ли ещё пары чисел, аналогичные паре 819 и 1221?

Период дроби 1/2017

Десятичная запись дроби 1/2017 имеет период длины 2016, т.е. 2017-1. Вообще, длина периода, равная n-1 - это наибольшее теоретически возможное значение для дроби 1/n.

Кто-то может сказать, что дробь 1/2017 даёт период длины 2016 из-за того, что оно простое. Однако, не для всех простых достигается максимальная возможная длина периода. Например, 1/3 = 0,(3) имеет период длины 1, а не 2.

Теорема 77

Возьмём число 11. Его можно представить как сумму 11  = 2 + 3 + 6. А если сложить величины, обратные этим слагаемым, то получим единицу:
$\frac{1}{2}+\frac{1}{3}+\frac{1}{6} = 1$

То же можно сделать и с числом, например, 24:
24 = 2 + 4 + 6 + 12
$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{12} = 1$

Некоторые же числа, например, 7, так разбить невозможно.

Оказывается, наибольшим числом, которое невозможно разбить на натуальные слагаемые таким образом, чтобы сумма их обратных величин была равной единице, является число 77. А для всех чисел, больших 77, такой способ существует.
Например, 78 = 2 + 6 + 8 + 10 + 12 + 40
$\frac{1}{2}+\frac{1}{6}+\frac{1}{8}+\frac{1}{10}+\frac{1}{12}+\frac{1}{40} = 1$

Теорема об этом была доказана в 1963 году Р.Грэхемом.

Период дроби делится на 9

Возьмём любое простое число, большее пяти. Найдём его обратную величину. Это будет бесконечная периодическая десятичная дробь.

Например, 1/7 = 0,(142857), 1/13 = 0,(076923), 1/31 = 0,(032258064516129).

Так вот, оказывается, что период, если его записать как натуральное число, будет всегда делиться на 9! (восклицательный знак здесь обозначает не факториал, а выражение эмоции :) )

На 9 делятся и число 142857, и число 76923 и 32258064516129.

Интересный факт? Расскажите, пожалуйста, о нашем блоге у себя - пусть больше читателей смогут открывать для себя занимательные математические факты.

Суперлуние и математика

Вот все пишут про суперлуние, а никто и не обратил внимание, что Луна сейчас находится ровно за тридевять Земель!

Если от поверхности Земли отложить 27 земных диаметров, то попадём на поверхность Луны!

Всем желающим предлагаю найти соответствующие параметры самостоятельно и определить, сильно ли я подогнал действительный результат под желаемый.

Ещё о правильно-неправильном сокращении дробей

Если сокращать дроби, зачёркивая одинаковые цифры, иногда можно получить правильный результат. Нашими читателями было найдено больше дробей с такими свойствами.

Оказывается все дроби с трёхзначными числителями и знаменателями, которые полностью сократятся при вычёркивании одинаковых цифр, есть в работе Boas, 1979 года.

Например: $\frac{124}{217} = \frac{4}{7}$, $\frac{316}{632} = \frac{1}{2}$. За полным списокм можете заглянуть по ссылке, а можете поискать самостоятельно.

А для программистов также будет интересно, что в 16-ричной системе подобных дробей с двузначными числителями и знаменателями целых 7, а не 4, как десятеричной.

Внимание. Ведущий блога не несёт ответственности, в случае, если читатели на контрольной по математике начнут сокращать так любые дроби. Например, $\frac{13}{39}$ не будет равняться $\frac{1}{9}$

Разбиение числа 24 на слагаемые

Число 24 можно разбить в сумму так, что сумма обратных величин этих слагаемых будет равна единице.

24 = 2+4+6+12

$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{12} = 1$

На math.hashcode.ru сейчас доказывают, что это верно и для любых натуральных чисел, превосходящих 24. Хотите присоединиться?

Объяснение математических часов: 5 - золотое сечение

На математических часах в двух формулах встречается буква фи ($\phi$) однако, она имеет разный смысл. Чётвёрка на часах задаётся через функцию Эйлера, а пятёрка - через константу Золотого сечения:

$5=(2\phi-1)^2$

5 - Золотое сечение
Золотое сечение возникает из следующей задачи. Единичный отрезок нужно разделить на 2 части так, чтобы большая часть относилась к меньшей как весь отрезок относится к его большей части.

Составим пропорцию:
$\frac{1-x}{x}=\frac{x}{1}$

Откуда получаем квадратное уравнение:
$x^2-x-1 = 0$

Его положительным корнем будет:
$x=\frac{1+\sqrt{5}}{2}$

Это число обозначается как $\phi\approx 1,618$

У него много интересных свойств. Например, если число фи увеличить на единицу, получим его квадрат. А если уменьшим на единицу - получим обратную величину, $\frac{1}{\phi}$

Число фи всплывает и при вычислении бесконечных цепных дробей или вложенных корней. Забавно, что собственно о числах Фибоначчи и порождающей их формуле я в блоге до сих пор не писал - постараюсь это исправить :)

Разность и сумма дробей

Разложение числа 2014 на простые множители поможет ответить и на вопрос, сколькими способами аликвотную дробь $\frac{1}{2014}$ можно представить в виде суммы или разности двух аликвотных дробей.

Составим диофантово уравнение:
$\frac{1}{x}-\frac{1}{y}=\frac{1}{2014}$

$\frac{y-x}{xy}=\frac{1}{2014}$

2014y - 2014x = xy

(2014-x)y = 2014x

$y = \frac{2014 x}{2014-x}$

Так как слева - натуральное число, то и справа число должно быть натуральным. Во-первых, такое возможно, если разность 2014 - х окажется равным одному из делителей числа 2014: 1, 2, 19, 38, 53, 106 или 1007. Это даёт пары решений (х,у):
(2013,4054182);
(2012,2026084);
(1995,211470);
(1976,104728);
(1961,74518);
(1908,36252);
(1007,2014).

Однако, все ли это решения? Нет, ведь, например, при x = 2010 знаменатель дроби $y = \frac{2014 x}{2014-x}$ тоже сократится полностью. Так как же найти, сколькими способами можно представить дробь $\frac{1}{2014}$ в виде разности двух аликвотных дробей, не прибегая к полному перебору?

Для этого введём замену d = 2014 - x. Тогда выражение для y обретёт вид:

$y = \frac{2014 (2014-d)}{d}=\frac{2014^2-2014d}{d}=\frac{2014^2}{d}-2014$

Таким образом, число d должно быть делителем числа $2014^2$ и быть меньше числа 2014. Всего для него 13 вариантов:
1, 2, 4, 19, 38, 53, 76, 106, 212, 361, 722, 1007, 1444

Что даёт следующие равенства:
$\frac{1}{2014}=\frac{1}{2013}-\frac{1}{4054182}=\frac{1}{2012}-\frac{1}{2026084}= \frac{1}{2010}-\frac{1}{1012035}=\\
=\frac{1}{1995}-\frac{1}{211470}=\frac{1}{1976}-\frac{1}{104728}=\frac{1}{1961}-\frac{1}{74518}=\\
=\frac{1}{1938}-\frac{1}{51357}=\frac{1}{1908}-\frac{1}{36252}=\frac{1}{1802}-\frac{1}{17119}=\\
=\frac{1}{1653}-\frac{1}{9222}=\frac{1}{1292}-\frac{1}{3604}=\frac{1}{1007}-\frac{1}{2014}=\frac{1}{570}-\frac{1}{795}$

А найти, сколькими способами число $\frac{1}{2014}$ представляется в виде суммы аликвотных дробей предлагаем вам самостоятельно. Будет хорошая тренировка перед математическими олимпиадами этого года.

Любые цифры в степени двойки

А вы знали, что для любой заданной наперёд последовательности цифр найдётся степень двойки, с этой последовательности начинающаяся? Например первые 4 цифры числа $2^{9645}$ будут 2718 - такие же, как и у числа e, а десятичная запись степени $2^{1363}$ начинается с 2013, номера текущего года.

Доказывается это вот как:

Злые числа

Если сложив от первой до некоторой n-й цифры дробной части числа x можно получить репдигит 666, то число x называют злым. Оказывается, злыми являются число пи и константа золотого сечения число фи. Требуемая сумма получается при складывании первых 144 или 146 цифр, соответственно.

Такое определение опять зависимо от выбранной системы счисления (кстати, в двоичной системе все иррациональные числа будут злыми). Но если рассмотреть аналогичным образом разложение числа в цепную дробь, от выбранной системы независящее, то и тут число пи окажется злым! Сумма первых 56 звеньев его цепной дроби даст 666.

Ряд Фарея

Если записать в порядке возрастания все дроби, которые получились при приближении числа е методом медиант, получим последовательность:




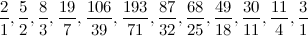
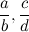Каждая дробь в ней равна медианте соседей. И для любых двух соседних дробей , произведения ad и bc отличаются на 1.

 Эта последовательность называется рядом Фарея.

Приближение числа обыкновенной дробью

Используя свойство медианты, можно находить рациональные приближения чисел. Покажем это на примере числа е .

Число е находится между двумя целыми числами:
2 < e < 3

Запишем границы в виде дробей:


Теперь сравним е с медиантой границ:


Значит, левую границу можно подвинуть:
 

Следующее сравнение с новой медиантой:
 

Снова уточняем оценку:
 

И продолжаем сравнивать число е с медиантой новый границ. В зависимости от результат сравнения будем пододвигать левую или правую границы:

 


Дальше буду писать только по одной границе для компактности:
 









Последнее приближение отличается от е всего на две стотысячных.

Взглянем на сам процесс приближения числа е через медианты внимательнее. Подсчитаем, сколько шагов проходило до того, как новая медианта оказывалась с другой стороны от числа. Получим: 1 дробь справа (e < 3), 2 дроби слева, 1 дробь справа, 1 дробь - слева, 4 дроби справа, 1 дробь - слева, 1 дробь - справа.

Но ведь это звенья разложения дробной части числа е в цепную дробь! [1, 2, 1, 1, 4, 1, 1 ...]

Вот и ещё один алгоритм разложения числа в цепную дробь, имеющий намного больший запас точности, чем периодическая замена дробной части числа обратной величиной.

Медианта

Медианта двух дробей - это такая дробь, числитель которой равен сумме их числителей, а знаменатель - сумме из знаменателей. Именно так пытаются складывать дроби дети, когда забывают (или не знают) об общем знаменателе :)

Оказывается, у такого действия много интересных применений. Всё потому, что величина медианты находится между величин образовавших её дробей. То есть:


Впервые термин этот ввёл в математику А.Я.Хинчин, тот самый, который открыл удивительную закономерность в цепных дробях.

Обобщённые цепные дроби

Если в числителях звеньев допускать не только единицы, а любые целые числа, получаются очень интересные разложения.

Например, число пи тогда можно представить так:


Красивая регулярная структура, не правда ли?

А корень из любого числа можно получить вот как:

Постоянная Хинчина

Если вы пробовали раскладывать наугад взятое число в цепную дробь, то, наверняка, обращали внимание, что единицы и двойки встречаются в разложении чаще всего, а большие числа - редко.

Этот факт в 1935 году заметил и советский математик Александр Яковлевич Хинчин. Он доказал, что почти для всех иррациональных чисел, предел среднего геометрического членов разложения их дробной части в цепную дробь будет величиной постоянной, и равной 2,685452...

Для иллюстрации этого процесса проведём его для дробной части числа пи:

Звено	Среднее геометрическое всех звеньев по данное
7	7
15	10,246951
1	4,717694
292	13,232535
1	7,894315
1	5,594510
1	4,374605
2	3,966891
1	3,403735
3	3,361030
1	3,010310
14	3,421666
2	3,283209
1	3,015922
1	2,801940
2	2,743513
2	2,692972
2	2,648829
2	2,609947
1	2,487712
84	2,941608
2	2,890471
1	2,760111

Однако, обратите внимание, что для пи ещё не доказано, будет ли в пределе именно постоянная Хинчина, 2,685452...

Известные исключения (для которых данный предел средних геометрических не получается) - это квадратичные иррациональности (с периодическими цепными дробями) и число е.

Периодические цепные дроби

Периодические цепные дроби получаются только из иррациональных чисел, являющихся корнями квадратного уравнения. Для всех остальных иррациональных чисел периода в цепочке не будет.

Вот, например:


 Или, в более компактном виде, это выглядит как:
[1; 3, 1, 5, 1, 1, 4, 1, 1, 8, 1, 14, 1, 10, 2, 1, 4, 12, 2, 3, 2, 1, 3, 4, 1, 1, 2, ...]

Но и среди непериодических цепных дробей встречаются имеющие красивые закономерности. Классический пример - число е, разложение которого - последовательные чётные числа, разделённые парами единиц.

[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, ...]

Цепная дробь из корня

Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существует способ получения цепной дроби любой длины, требующий лишь ручки и бумаги. Разложим с его помощью корень из 503, который нам был нужен для решения уравнения Пелля.

 Для начала выделим в корне целую часть. Так как 22² = 484, а 23² = 529, то


 Итак, искомое разложение начнётся как [22, ....]

 Превратим дробную часть в дробь с числителем 1:
 

 Избавимся от иррациональности в знаменателе дроби, воспользовавшись тем, что:


 Получим:


 Теперь выделим у дроби целую часть:
 

 Получили второй член разложения: [22, 2, ....] А в целом цепная дробь сейчас выглядит так:
 

Перевернём теперь дробную часть ещё раз:


 Внимание! Здесь начинается особая математическая магия! Дело в том, что знаменатель обязательно должен разделиться на целый множитель числителя. Очень рекомендую это доказать - удовольствие гарантировано.

 Действительно, здесь тоже имеем:
 

 И выделение целой части даёт нам новый член разложения: [22, 2, 2, ....]

 Вот новое звено цепной дроби:
   

Данный процесс можно продолжать. Когда получим на каком-либо шаге дробь, которая получалась ранее (а мы обязательно получим такую, это тоже можно доказать), соответствующий участок разложения зациклится.

 Вот так можно получить цепную дробь любого корня без каких-либо электронных вычислительных средств. А вообще, самый простой способ - это вбить в ВольфрамАльфе: continued fraction, а затем в новом открывшемся окошке написать sqrt(503)

Как получить цепную дробь

При решении уравнения Пелля для нахождения рациональных приближений иррационального числа, то мы раскладывали в цепную дробь. А как, собственно, это делается?

Допустим, в цепную дробь мы хотим разложить число пи = 3,14159265358... Для начала выделим целую часть:


Затем дробную часть заменим дробью с единицей в числителе:


Теперь выполним это же действие с числом в знаменателе


И ещё раз, и ещё:


Полученная цепная дробь будет бесконечной и непериодической.

В более компактном виде это запишется как:
[3, 7, 15, 1, 292, 1, 1, 1, 2,...]

Кстати, при таком способе разложения скоро даёт о себе знать точность калькулятора, и начинаются ошибки. Например, если вычисления вести в Экселе, то для числа пи можно найти лишь 13 верных звеньев.

Уравнение Пелля

Рассмотрим задачу:
Найти натуральные x и y, для которых
 x² - 2012y² = 1

Поскольку 2012 кратно четырём, то данное уравнение равносильно:
 x² - 503z² = 1,
где z = 2y.

Вот, что с ним можно сделать теперь . Разделим обе части на z² и выполним перенос вычитаемого вправо:


И извлечём корень:


Таким образом, корни этого диофантова уравнения можно искать среди рациональных приближений корня из 503.

Этот корень раскладывается в бесконечную цепную дробь:


Дальше числа в знаменателях будут периодично повторяться. Более коротко такая цепная дробь записывается как:
[22, (2, 2, 1, 21, 1, 2, 2, 44)].

Если обрывать цепную дробь на каком-нибудь слагаемом и сворачивать её обратно, будем получать подходящие дроби. Если для приближения взять дробь



То получим первую пару натуральных чисел, удовлетворяющую условию:
24648² - 503*1099² = 1

Таким образом, x = 24648, y = 2198

Вот так решаются уравнения Пелля. Заметим. что в таких уравнениях коэффициент при y² не является полным квадратом.