Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат.
Что если попробовать плавной линией соединить эти точки и найти функцию, график которой имел бы такой вид? Тогда можно было бы вычислять факториал от любых чисел, не только от натуральных.
Об этом математики задумались в начале XVIII века. Если такая функция f(x) существует, она должна удовлетворять условию f(x) = x f(x-1), т.е. рекурсивному определению факториала. В 1729 году Леонард Эйлер нашёл способ получить факториал в виде бесконечного произведения, в которое в качестве аргумента можно было подставлять и дробные числа.
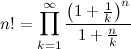
Вот как будет работать эта формула для n = 4, например:
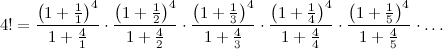
Сходится произведение довольно медленно, я проверил в Экселе. Для того, чтобы произведение превысило 23, нужно взять 139 множителей, а чтобы добраться до 23,5, множителей нужно уже 283. На 1435-м шагу произведение доходит до 23,4, ну а в бесконечности будет равно 24
Я выложил лист для вычисления факториала в гугл доки. Меняете n и смотрите, к чему будут стремиться частичные произведения.
Чуть позже Эйлер выразил факториал в виде несобственного интеграла:
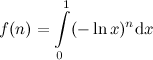
Применим к нему метод интегрирования частями, взяв u = (-ln x)n, dv = dx:
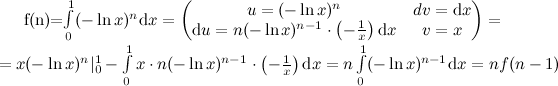
Требуемое свойство выполняется.
Заменой t = −ln x этот интеграл принимает используемый в настоящее время вид и известен как гамма-функция.
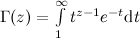
Аргументами её могут быть не только дробные или даже отрицательные числа, но и комплексные.
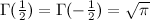
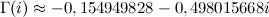
Для натуральных аргументов Г(n) = (n-1)!
Шотландский математик Джеймс Стирлинг был современником Эйлера и вывел формулу, позволяющую приближённо вычислять факториал для больших чисел.
Об этом математики задумались в начале XVIII века. Если такая функция f(x) существует, она должна удовлетворять условию f(x) = x f(x-1), т.е. рекурсивному определению факториала. В 1729 году Леонард Эйлер нашёл способ получить факториал в виде бесконечного произведения, в которое в качестве аргумента можно было подставлять и дробные числа.
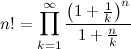
Вот как будет работать эта формула для n = 4, например:
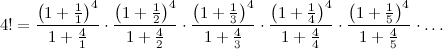
Сходится произведение довольно медленно, я проверил в Экселе. Для того, чтобы произведение превысило 23, нужно взять 139 множителей, а чтобы добраться до 23,5, множителей нужно уже 283. На 1435-м шагу произведение доходит до 23,4, ну а в бесконечности будет равно 24
Я выложил лист для вычисления факториала в гугл доки. Меняете n и смотрите, к чему будут стремиться частичные произведения.
Чуть позже Эйлер выразил факториал в виде несобственного интеграла:
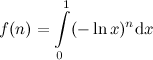
Применим к нему метод интегрирования частями, взяв u = (-ln x)n, dv = dx:
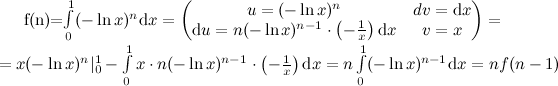
Требуемое свойство выполняется.
Заменой t = −ln x этот интеграл принимает используемый в настоящее время вид и известен как гамма-функция.
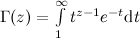
Аргументами её могут быть не только дробные или даже отрицательные числа, но и комплексные.
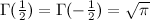
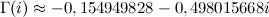
Для натуральных аргументов Г(n) = (n-1)!
Шотландский математик Джеймс Стирлинг был современником Эйлера и вывел формулу, позволяющую приближённо вычислять факториал для больших чисел.
А вот как я использовал факториал на математических часах.





Блестяще! Эйлер и тут постарался. Математик-универсал.
ОтветитьУдалитьТолько, кажется, я опечатку нашёл в формуле с произведением. Там оно идёт по k, а не по n.
ОтветитьУдалитьСпасибо большое, поправил.
УдалитьДа, математики Нового времени были гигантами, универсалами, можно сказать :) Последним универсалом был Пал Эрдеш, уже почти наш своременник, у которого были работы во множестве областей. А сейчас математика всё больше расслаивается с пециалисту по теории графов будет сложно вникнуть, скажем, в то, что происходит на переднем краю дифуров.
О, да, нынче не такие. Каюсь, сам весьма многого не знаю.
УдалитьСейчас вот остро потребовалось изучить исследование операций, в котором я никак не ориентируюсь, так много нового открою для себя :)
Классическая книга по этой теме за аторством Вентцель Елены Сергеевны.
Удалить