Мы привыкли доверять в расчётах компьютеру. Но иногда - чересчур полагаемся на него. А сейчас я покажу один поучительный пример, позволяющий оценить точность вычислений.
Откроем новый документ Excel. В ячейку А1 введём число 0
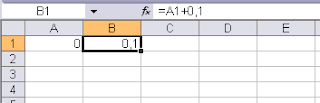
В ячейку В1 введём формулу:
=A1+0,1
Нажав Enter, получим число 0,1 в ячейке - всё правильно.
Теперь размножим эту формулу до ячейки К1, потянув мышкой за правый нижний угол ячейки В1:
И здесь всё нормально - строка заполнилась числами от 0 до 1 с шагом в одну десятую:
Ничего, скоро всё будет :) Ещё один шаг - в ячейку А1 вводим формулу
=4*А1*(1-А1)
Мы должны получить 4*0*(1-0) = 0. Мы его там и получаем. Но возьмём и размножим теперь вправо формулу из ячейки А2 до я чейки К2.
Как вы думаете, какие числа окажутся в ячейках с В2 по К2? Можно прикинуть на калькуляторе. Например, в В2 будет число 4*0,1*(1-0,1) = 0,4*0,9 = 0,36
В ячейке F2 должно быть число 4*0,5*(1-0,5) = 2*0,5 = 1
А в ячейке К2 должзно быть число 4*1*(1-1) = 4*0 = 0
Но наш прогноз оправдался везде, кроме ячейки К2:
Там находится число чуть большее нуля (ошибка в 16-м знаке после запятой). Казалось бы, мелочь, но если мы теперь размножим всю строку вниз, ошибка продолжит накапливаться и скоро число в столбце К уже станет тысячными, десятыми и приблизится к единице.
Попробуйте провести аналогичные действия в своём табличном редакторе. Для сравнения можете указать в комментариях, на какой строке число в столбце К превысит 0,1 и в какой программе/версии это выполнялось.
Я проводил эксперимент в Excel 2003 (11.6560.6568) SP2
Откроем новый документ Excel. В ячейку А1 введём число 0
В ячейку В1 введём формулу:
=A1+0,1
Нажав Enter, получим число 0,1 в ячейке - всё правильно.
Теперь размножим эту формулу до ячейки К1, потянув мышкой за правый нижний угол ячейки В1:
И здесь всё нормально - строка заполнилась числами от 0 до 1 с шагом в одну десятую:
Ничего, скоро всё будет :) Ещё один шаг - в ячейку А1 вводим формулу
=4*А1*(1-А1)
Мы должны получить 4*0*(1-0) = 0. Мы его там и получаем. Но возьмём и размножим теперь вправо формулу из ячейки А2 до я чейки К2.
В ячейке F2 должно быть число 4*0,5*(1-0,5) = 2*0,5 = 1
А в ячейке К2 должзно быть число 4*1*(1-1) = 4*0 = 0
Но наш прогноз оправдался везде, кроме ячейки К2:
Попробуйте провести аналогичные действия в своём табличном редакторе. Для сравнения можете указать в комментариях, на какой строке число в столбце К превысит 0,1 и в какой программе/версии это выполнялось.
Я проводил эксперимент в Excel 2003 (11.6560.6568) SP2
В A1 введите «0,7». В B1 — «=A1 * 11 - 7». А потом протяните B1 вниз строк, этак, на 30. ;) Так, по-моему, зрелищнее.
ОтветитьУдалитьКрасота!
УдалитьУ меня в минус ушло на 17-й ячейке.
Кстати, в разных версиях программы результат будет, скорее всего одинаковым, так как это особенность конкретного продукта, а свойство чисел с плавающей точкой конечной точности.
ОтветитьУдалитьНу и непредставимость одной десятой в виде конечной двоичной дроби тоже играет свою роль.
Nonetheless, done skillfully over a long period of time,
ОтветитьУдалитьtwo colluding players can gain an advantage over the rest of the table.
If you are new to copying PS3 games and you don’t yet know how to do this you
will be pleased to know that the process has now been made very easy by
the availability of reliable copy software which can be downloaded.
This is your other tank in Warhammer online, special ability is buffs.
Here is my web blog; board.yet-another-server.com
my website :: spielen
О, спам появился - значит, блог набирает популярность :)
УдалитьПредлагаю ещё один пример - http://my-tribune.blogspot.ru/2013/02/accuracy.html (там вообще за 5 шагов набираем ощутимую ошибку).
ОтветитьУдалитьКрасиво! Пожалуй, именно в таком виде буду курсантам своим показывать.
ОтветитьУдалитьПриветствую, general.
ОтветитьУдалитьЭто, конечно, интересно находить темные пятна на продукции Microsoft, но в 1 очередь нужно уяснить, что мы вообще хотим от Excel? Перед создателями табличного процессора Excel, в том числе, стояла задача создать приложение с минимальными требованиями к персональному компьютеру, чтобы даже пользователь с древним компьютером мог пользоваться их продуктом. Конечно же они могли хранимую в ячейке точность повысить до 10^308 точности, но представьте, какая производительность требовалась бы тогда? Но это все лирика.
Пользователь должен для себя решить, что он хочет получить в результате. Если бы мы хотели, в данном примере, вывести точный результат, то следовало выбрать в меню: Сервис -- Параметры Excel -- Дополнительно -- Задать точность как на экране. Погрешность в таком случае накапливаться не будет, мы поучим требуемый результат.
Далее,нужно защитить себя от необдуманных действий, которые могут привести к ошибке. В данном случае нужно было в ячейку А1 вбить 0, в ячейку В1 вбить 0,1 и растянуть и действовать как описано выше. В таком случае результат будет верным.
То, что мы видим в тексте выше, умышленное накопление погрешности, ее нетрудно оценить.
Сергей, рад видеть у себя!
УдалитьДа, для тех, кто знает, как хранятся числа в компьютере - это не секрет, а если кто раньше не задумывался об этом, будет открытием (вместе с Вашим комментарием и ещё более интересным).
А вот, вспомнил, был у меня ещё забавный случай с Excel'ем из серии, что называется, "нарочно не придумаешь" :)
Прочитал. Любопытный случай =)
УдалитьТочность хранимых значений в Excel 15 знаков (1*10^(-15)). Создавая рекурсию (производя арифметические операции с предыдущей ячейкой, имеющую погрешность погрешностью 1*10^(-15) ) мы ее как минимум удваиваем, т.е. на 10 обращении точность падает в 2^10=1024 что примерно 10^3, т.е. уже на 3 знака. А если это 4, то 4^10=2^20=1048576 что примерно 10^6, т.е. на 6 знаков (точность уменьшается до 1*10^(-9)). Так вот, чтобы не получать ошибочные результаты, нужно избегать рекурсивных вызовов, использовать округление результатов до требуемой точности в промежуточных расчетах и т.п.
ОтветитьУдалить