При решении уравнения Пелля для нахождения рациональных приближений иррационального числа, то мы раскладывали в цепную дробь. А как, собственно, это делается?
Допустим, в цепную дробь мы хотим разложить число пи = 3,14159265358... Для начала выделим целую часть:
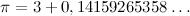
Затем дробную часть заменим дробью с единицей в числителе:
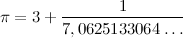
Теперь выполним это же действие с числом в знаменателе
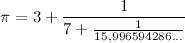
И ещё раз, и ещё:
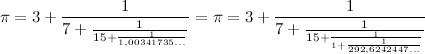
Полученная цепная дробь будет бесконечной и непериодической.
В более компактном виде это запишется как:
[3, 7, 15, 1, 292, 1, 1, 1, 2,...]
Кстати, при таком способе разложения скоро даёт о себе знать точность калькулятора, и начинаются ошибки. Например, если вычисления вести в Экселе, то для числа пи можно найти лишь 13 верных звеньев.
Допустим, в цепную дробь мы хотим разложить число пи = 3,14159265358... Для начала выделим целую часть:
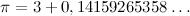
Затем дробную часть заменим дробью с единицей в числителе:
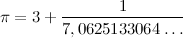
Теперь выполним это же действие с числом в знаменателе
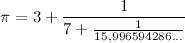
И ещё раз, и ещё:
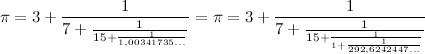
Полученная цепная дробь будет бесконечной и непериодической.
В более компактном виде это запишется как:
[3, 7, 15, 1, 292, 1, 1, 1, 2,...]
Кстати, при таком способе разложения скоро даёт о себе знать точность калькулятора, и начинаются ошибки. Например, если вычисления вести в Экселе, то для числа пи можно найти лишь 13 верных звеньев.


Комментариев нет:
Отправить комментарий