Площадь треугольника, зная его стороны, можно найти по формуле Герона.
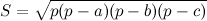 <
<
Где a, b, c - стороны треугольника, а p - полупериметр.
Для данного треугольника p=21 и формула даст в результате
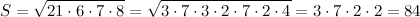
Таким образом, площадь его выражается целым числом.
Другой треугольник, стороны которого - последовательные натуральные числа, а площадь целая - это египетский треугольник со сторонами 3, 4, 5 и площадью 6.
Существуют ли ещё треугольники с таким свойством?
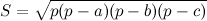 <
<Где a, b, c - стороны треугольника, а p - полупериметр.
Для данного треугольника p=21 и формула даст в результате
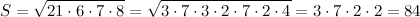
Таким образом, площадь его выражается целым числом.
Другой треугольник, стороны которого - последовательные натуральные числа, а площадь целая - это египетский треугольник со сторонами 3, 4, 5 и площадью 6.
Существуют ли ещё треугольники с таким свойством?




Нужно будет проверить сейчас.
ОтветитьУдалитьКстати, эту же формулу можно использовать и для нахождения площади вписанного в окружность четырёхугольника (с произвольными сторонами).
S^2 = (p-a)(p-b)(p-c)(p-d)
Интересно, спасибо :)
ОтветитьУдалитьТаких море: 4, 13, 15; 5, 5, 6; 5, 5, 8; 5, 12, 13; 7, 15, 20; 8, 15, 17; 9, 10, 17; 16, 17, 17 и т. д.
ОтветитьУдалитьДа, с целыми сторонами и целой площадью много, а вот если стороны - последовательные натуральные числа?
УдалитьТогда это 51, 52, 53; 193, 194, 195; 723, 724, 725; 2701, 2702, 2703; 10083, 10084, 10085; 37633, 37634, 37635.
Удалить