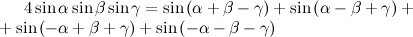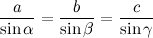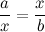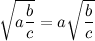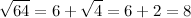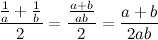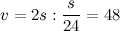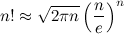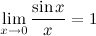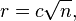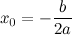Перед Новым Годом на математических форумах вновь обретает популярность развлечение: составить из цифр 2, 0, 1 и 1 математическое выражение, значение которого равнялось бы равнялось бы некоторому наперёд заданному числу. Если в помощью четырёх знаков действий, возведения в степень и квадратного корня это оказывается сделать затруднительно, на помощь приходят более экзотические функции, например, праймориал.
Праймориал числа n - это произведение всех простых чисел, не превосходящих n. Обозначается он решёткой #. Например, праймориал 20-ти равен:
20# = 2 * 3 * 5 * 7 * 11 * 13 * 17 * 19 = 9699690
Интересные числа, занимательные математические факты и удивительные конструкции. Узнавайте каждый день что-то новое!
вторник, 27 декабря 2011 г.
суббота, 24 декабря 2011 г.
5 цифр
Наш постоянный читатель и комментатор Николай составил выражение, в которое входят цифры от 1 до 5, и результатом которого является 2012, номер будущего года:
452 - 13
С цифрами от 0 до 5 получается следующее:
4 * 502 + 1 + 3
452 - 13
С цифрами от 0 до 5 получается следующее:
4 * 502 + 1 + 3
пятница, 23 декабря 2011 г.
Снежное дерево
Так хочется настоящего снега этой зимой! И я написал флеш-игру, которая использует те же алгоритмы, что и моя программа для снегопада на рабочем столе.
Двигая зажатой кнопкой мыши вы создаёте воздушные потоки, которые несут с собой снежинки. Достигнув земли, снежинки начинают формировать дерево. Цель игры - вырастив дерево, собрать висящие в воздухе подарки.
Сейчас игра участвует в конкурсе на двух сайтах, там можно поиграть и, если понравится, поддержать.
Вот - http://www.kongregate.com/games/GeneralVimes/snow-tree
и вот - http://www.newgrounds.com/portal/view/586449
Двигая зажатой кнопкой мыши вы создаёте воздушные потоки, которые несут с собой снежинки. Достигнув земли, снежинки начинают формировать дерево. Цель игры - вырастив дерево, собрать висящие в воздухе подарки.
Сейчас игра участвует в конкурсе на двух сайтах, там можно поиграть и, если понравится, поддержать.
Вот - http://www.kongregate.com/games/GeneralVimes/snow-tree
и вот - http://www.newgrounds.com/portal/view/586449
четверг, 22 декабря 2011 г.
2 + 2 = 5
Сейчас в блоге всего две записи в категории софизмы: с извлечением корня и интегрированием частями.
Но самый популярный математический софизм использует неявное деление на 0. И хотя многим он напомнит о русском крейсере, всё же запосчу.
Начнём с очевидного равенства
5 - 4 = 1
Умножим левую и правую часть его на единицу:
(5 - 4)(5 - 4) = 1(5 - 4)
Раскроем скобки, не приводя подобные:
5*5 - 5*4 - 5*4 + 4*4 = 1*5 - 1*4
Преобразовываем:
5*5 - 5*4 + 4*4 = 5*4 + 1*5 - 1*4
5*5 - 5*4 = 5*4 + 1*5 - 4*4 - 1*4
5*5 - 5*4 - 1*5 = 5*4 - 4*4 - 1*4
Выносим общий множитель за скобки:
5(5 - 4 - 1) = 4(5 - 4 - 1)
И сокращаем:
5 = 4
Но самый популярный математический софизм использует неявное деление на 0. И хотя многим он напомнит о русском крейсере, всё же запосчу.
Начнём с очевидного равенства
5 - 4 = 1
Умножим левую и правую часть его на единицу:
(5 - 4)(5 - 4) = 1(5 - 4)
Раскроем скобки, не приводя подобные:
5*5 - 5*4 - 5*4 + 4*4 = 1*5 - 1*4
Преобразовываем:
5*5 - 5*4 + 4*4 = 5*4 + 1*5 - 1*4
5*5 - 5*4 = 5*4 + 1*5 - 4*4 - 1*4
5*5 - 5*4 - 1*5 = 5*4 - 4*4 - 1*4
Выносим общий множитель за скобки:
5(5 - 4 - 1) = 4(5 - 4 - 1)
И сокращаем:
5 = 4
среда, 21 декабря 2011 г.
Масла в огонь
В копилку страхов и предсказаний, связанных с 2012 годом, добавил ещё одно забавное свойство наш читатель Николай.
Разделим жуткое число 2012 на не менее жуткое число 666. В результате в целой части будет 3, далее после запятой идёт 0, а затем будут цифры 2, 1, 0, 2, т.е. само число 2012, записанное наоборот!
2012 / 666 = 3,02102...
Разделим жуткое число 2012 на не менее жуткое число 666. В результате в целой части будет 3, далее после запятой идёт 0, а затем будут цифры 2, 1, 0, 2, т.е. само число 2012, записанное наоборот!
2012 / 666 = 3,02102...
4 квадрата
Чтобы получить число 2011, нужно 3 квадрата, об этом мы уже писали. А для числа 2012 даже трёх квадратов недостаточно, их нужно целых четыре!
Вот, например, так:
2012 = 332+272+132+52
Всего будет 39 подобных способов, из которых в 24 случаях все слагаемые различны.
Вот, например, так:
2012 = 332+272+132+52
Всего будет 39 подобных способов, из которых в 24 случаях все слагаемые различны.
пятница, 16 декабря 2011 г.
Боначчиевич
В прозвище Леонардо Пизанского, гениального математика Средневековья, часто норовят удвоить первую букву б и написать его "Фиббоначчи". Избежать подобной ошибки поможет знание того, что Фибоначчи - это на самом деле отчество и изначально писалось раздельно: filius Bonacci, т.е. сын Боначчи. Есть и другая версия его происхождения, но и в ней первое "Фи" означает "сын". Да и сейчас сын по-итальянски будет figlio (фильо).
А весной я писал о том, как запомнить правила правописания некоторых математических терминов.
А весной я писал о том, как запомнить правила правописания некоторых математических терминов.
вторник, 13 декабря 2011 г.
Устный счёт
Сегодня на Хабре avfonarev рассказал о своём приложении для iPad, в котором предлагается решать задачи в уме. Основано оно на задачнике Сергея Александровича Рачинского.
И хотя про саму картину, изображаюoe. его урок, я знал давно, даже хотел использовать как один из уровней в своей игре, о самом Рачинском и его задачнике когда-то, наверняка, читал, но забыл.
А задачник этот, «1001 задача для умственного счета», и основанное на нём приложение, оказались весьма полезными сейчас для тренировки мозгов, привыкших к калькуляторам.
Вот пример задачи оттуда, попробуйте решить устно:
У меня под огородом 1 десятина. В нем картофель занимает в 7 раз больше места, чем капуста, капуста в 7 раз больше, чем горох, горох в 7 раз больше, чем лук, а именно лук занимает 1 грядку шириною в 2 аршина. Как длинна эта грядка?
1 десятина = 2400 кв.саженям
1 сажень = 3 аршина
У меня получилось :) Кстати, года 2 назад я писал пост об онлайн-библиотеках, где можно найти материалы для подготовки к олимпиадам. Задачник оттуда тоже можно скачать.
И хотя про саму картину, изображаюoe. его урок, я знал давно, даже хотел использовать как один из уровней в своей игре, о самом Рачинском и его задачнике когда-то, наверняка, читал, но забыл.
А задачник этот, «1001 задача для умственного счета», и основанное на нём приложение, оказались весьма полезными сейчас для тренировки мозгов, привыкших к калькуляторам.
Вот пример задачи оттуда, попробуйте решить устно:
У меня под огородом 1 десятина. В нем картофель занимает в 7 раз больше места, чем капуста, капуста в 7 раз больше, чем горох, горох в 7 раз больше, чем лук, а именно лук занимает 1 грядку шириною в 2 аршина. Как длинна эта грядка?
1 десятина = 2400 кв.саженям
1 сажень = 3 аршина
У меня получилось :) Кстати, года 2 назад я писал пост об онлайн-библиотеках, где можно найти материалы для подготовки к олимпиадам. Задачник оттуда тоже можно скачать.
воскресенье, 11 декабря 2011 г.
Четырёхзначные числа
Существует ровно 2012 четырёхзначных числа, которые не делятся ни на одну из своих цифр.
суббота, 10 декабря 2011 г.
пятница, 9 декабря 2011 г.
Троичная система
Т.к. все цифры в записи числа 2012 меньше трёх, то его можно рассмотреть как запись некоторого числа в троичной системе. Таким числом будет 2x33+0x32+1x31+2x30=54+3+2=59.
Кстати, простое число 59 является решением одного из вариантов задачи о раскладывании предметов:
Торговка пыталась разложить яйца поровну в 2, 3, 4, 5 или 6 корзин, но каждый раз оставались лишними 1, 2, 3, 4 или 5 яиц, соответственно. Найдите их наименьшее возможное количество.
А каким бы был ответ задачи, если бы при таком раскладывании всегда оставалось одно лишнее яйцо и корзины бы не оказывались пустыми?
Кстати, простое число 59 является решением одного из вариантов задачи о раскладывании предметов:
Торговка пыталась разложить яйца поровну в 2, 3, 4, 5 или 6 корзин, но каждый раз оставались лишними 1, 2, 3, 4 или 5 яиц, соответственно. Найдите их наименьшее возможное количество.
А каким бы был ответ задачи, если бы при таком раскладывании всегда оставалось одно лишнее яйцо и корзины бы не оказывались пустыми?
четверг, 8 декабря 2011 г.
Степени двойки
Все цифры числа 2012 являются или степенью двойки или нулём. Это же свойство имеет и квадрат числа 2012, число 4048144.
среда, 7 декабря 2011 г.
Нули и единицы
Оказывается, существует ровно 2012 последовательностей из 12 нулей и единиц, в которых группа цифр 001 встречается только 1 раз.
Также в 2012 последовательностях из 12 нулей и единиц будут равное число раз встречаться группы 0001 и 0100.
А если рассмотреть последовательности длины 13, то в 2012 из них не найдётся ни 0001, ни 0011.
Также в 2012 последовательностях из 12 нулей и единиц будут равное число раз встречаться группы 0001 и 0100.
А если рассмотреть последовательности длины 13, то в 2012 из них не найдётся ни 0001, ни 0011.
вторник, 6 декабря 2011 г.
Венера
Кроме уже указанных астрономически-календарных свойств 2012 года, в нём произойдёт ещё одно замечательное событие: прохождение Венеры по диску Солнца.
Оно случится 6 июня. Предыдущий раз это было в 2004 году, а следующий наступит аж в 2117.
Оно случится 6 июня. Предыдущий раз это было в 2004 году, а следующий наступит аж в 2117.
понедельник, 5 декабря 2011 г.
2012!
В факториале числа 2012 содержится 5776 цифр, это квадрат числа 76.
Такое, чтобы количество цифр в факториале номера года было полным квадратом, в прошлый раз случалось в 1921 году, а следующий раз будет только в 2105 году.
Кстати, число 76 интересно само по себе также тем, любая его степень оканчивается на 76. Из двузначных чисел таким свойством обладает также число 25. А существуют ли трёхзначные числа, которые совпадают с трёхциферными окончаниями своих степеней?
Такое, чтобы количество цифр в факториале номера года было полным квадратом, в прошлый раз случалось в 1921 году, а следующий раз будет только в 2105 году.
Кстати, число 76 интересно само по себе также тем, любая его степень оканчивается на 76. Из двузначных чисел таким свойством обладает также число 25. А существуют ли трёхзначные числа, которые совпадают с трёхциферными окончаниями своих степеней?
пятница, 2 декабря 2011 г.
8
По-английски 8 (eight) произносится так же как и глагол "съесть" в прошедшем времени (ate). На этом основана английская шутка:
- Почему шестёрка боится семёрки?
- Потому, что 7, 8, 9!
(по английски 7, 8, 9 звучит как seven ate nine, т.е. семёрка съела девятку).
- Почему шестёрка боится семёрки?
- Потому, что 7, 8, 9!
(по английски 7, 8, 9 звучит как seven ate nine, т.е. семёрка съела девятку).
четверг, 1 декабря 2011 г.
Как сложить числа
Когда был Гаусс маленький, с кудрявой головой...
В общем, великий математик Карл Фридрих Гаусс, тоже учился в школе. В школе этой в одном классе занимались дети разных лет. И вот, чтобы надолго занять малышей, учитель предложил им подсчитать сумму всех чисел от 1 до 100: 1+2+3+...+100.
Но пока учитель диктовал условие, маленький Гаусс уже быстро сообразил, что суммы крайних чисел в этой последовательности постоянны: 1+100=2+99=3+98=...=50+51=101. И, так как таких пар будет 50, искомый результат равен 5050.
Впрочем, эту историю наверняка вы уже где-то читали. А кто тогда сможет сказать, что это за крейсер?
В общем, великий математик Карл Фридрих Гаусс, тоже учился в школе. В школе этой в одном классе занимались дети разных лет. И вот, чтобы надолго занять малышей, учитель предложил им подсчитать сумму всех чисел от 1 до 100: 1+2+3+...+100.
Но пока учитель диктовал условие, маленький Гаусс уже быстро сообразил, что суммы крайних чисел в этой последовательности постоянны: 1+100=2+99=3+98=...=50+51=101. И, так как таких пар будет 50, искомый результат равен 5050.
Впрочем, эту историю наверняка вы уже где-то читали. А кто тогда сможет сказать, что это за крейсер?
суббота, 26 ноября 2011 г.
Восстановите шедевры живописи
Сегодня в большой интернет я выпустил свою новую игру, Save the Paintings. В ней вам нужно спасти всемирно известные картины, которые внезапно исчезли.
Умение рисовать не нужно - главное правильно расположить элементы.
Игра есть здесь и здесь. На обоих порталах проходит конкурс и, если игра понравится, можно поддержать её своими голосами.
Умение рисовать не нужно - главное правильно расположить элементы.
Игра есть здесь и здесь. На обоих порталах проходит конкурс и, если игра понравится, можно поддержать её своими голосами.
пятница, 25 ноября 2011 г.
Три простых множителя
Число 2012 открывает серию из четырёх чисел, каждое из которых представляется в виде произведения ровно трёх простых.
2012 = 2 * 2 * 503
2013 = 3 * 11 * 61
2014 = 2 * 19 * 53
2015 = 5 * 13 * 31
А существуют ли более длинные серии из подобных чисел?
2012 = 2 * 2 * 503
2013 = 3 * 11 * 61
2014 = 2 * 19 * 53
2015 = 5 * 13 * 31
А существуют ли более длинные серии из подобных чисел?
четверг, 24 ноября 2011 г.
Вставляем цифры
Если в простое число 999997600699 в начало, конец и между каждой парой цифр добавить одинаковые нечётный цифры: 1, 3, 7 или 9, полученное число будет простым.
Числа
1919191919171610101619191,
3939393939373630303639393,
7979797979777670707679797,
9999999999979690909699999 - простые.
Число нашёл Anton Vrba на PrimePuzzles.net
Числа
1919191919171610101619191,
3939393939373630303639393,
7979797979777670707679797,
9999999999979690909699999 - простые.
Число нашёл Anton Vrba на PrimePuzzles.net
среда, 23 ноября 2011 г.
Календарь-додекаэдр
На Хабрахабре passerby опубликовал ссылку на свой генератор календарей. Этот генератор может составлять календари в различных системах счисления, а также располагать их как на обычных прямоугольных листах, так и на развёртках многогранников.
вторник, 22 ноября 2011 г.
Маршруты шахматного коня
Известна задача об обходе всех полей доски n x m шахматным конём. У неё есть интересная вариация: эту доску нужно обойти конём, сделав максимально возможное число шагов так, чтобы маршрут не содержал пересекающихся участков.
Эту задачу успешно решают для всё больших и больших значений n и m мои коллеги Наталия Макарова (также исследовательница магических квадратов) и Алексей Чернов. Результаты представлены в базе данных. Вот, например, один из двух вариантов замкнутого пути по обычной шахматной доске 8 на 8:
Кроме коня там также есть база данных путей фантастических фигур: жирафа (ходит на 3 клетки в одном направлении и 1 в другом), зебры (3 и 2 клетки, соответственно) и антилопы (4, 3). Все, желающие принять участие в исследованиях, могут пополнять эту базу своими результатами.
Эту задачу успешно решают для всё больших и больших значений n и m мои коллеги Наталия Макарова (также исследовательница магических квадратов) и Алексей Чернов. Результаты представлены в базе данных. Вот, например, один из двух вариантов замкнутого пути по обычной шахматной доске 8 на 8:
Кроме коня там также есть база данных путей фантастических фигур: жирафа (ходит на 3 клетки в одном направлении и 1 в другом), зебры (3 и 2 клетки, соответственно) и антилопы (4, 3). Все, желающие принять участие в исследованиях, могут пополнять эту базу своими результатами.
понедельник, 21 ноября 2011 г.
воскресенье, 20 ноября 2011 г.
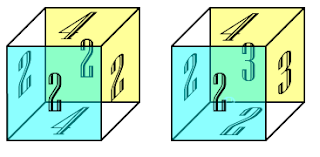
Теорема Пифагора
Среди многочисленных доказательств теоремы Пифагора особенно наглядны те, где квадраты, построенные на катетах разрезаются на части и из этих частей формируется квадрат, построенный на гипотенузе.
Вот один из таких способов, указанных в англоязычной Википедии:
Кстати, почти всегда англоязычные математические статьи в Википедии полнее и интереснее русскоязычных. имейте это в виду, если ищете информацию. А если есть возможность и время - можете помочь русскоязычному разделу, пополняя его переводами с английского.
Вот один из таких способов, указанных в англоязычной Википедии:
Кстати, почти всегда англоязычные математические статьи в Википедии полнее и интереснее русскоязычных. имейте это в виду, если ищете информацию. А если есть возможность и время - можете помочь русскоязычному разделу, пополняя его переводами с английского.
суббота, 19 ноября 2011 г.
Разрезание пиццы
Прочитал у Константина Кнопа, что если выбрать в круглой пицце произвольную точку и провести из неё разрезы через 45 градусов, то сумма площадей чётных частей будет равна сумме площадей нечётных частей.
Интересно, подумаю над доказательством.
Интересно, подумаю над доказательством.
пятница, 18 ноября 2011 г.
Преобразовать произведение синусов в сумму
Формула преобразования произведения двух синусов в сумму изучается в школе. А иногда требуется преобразовать в сумму произведение трёх синусов.
Конечно же, это можно сделать, дважды применив формулу для двух аргументов, однако формула для трёх синусов сама по себе достаточно красивая и мне захотелось привести её здесь.
На саму формулу я наткнулся в статье о целочисленных углах.
Конечно же, это можно сделать, дважды применив формулу для двух аргументов, однако формула для трёх синусов сама по себе достаточно красивая и мне захотелось привести её здесь.
На саму формулу я наткнулся в статье о целочисленных углах.
четверг, 17 ноября 2011 г.
2012
Потихоньку собираю информацию об интересных свойствах числа 2012, номере будущего года. Оказывается, в 2012 году будет 3 пятницы, выпадающих на 13-е число. Предыдущий раз такое случалось в 2009 году. И так же, как и в 2009, в 2012 году будет месяц, в котором дважды произойдёт полнолуние.
А начнётся год с воскресенья, как и 2006-й.
А начнётся год с воскресенья, как и 2006-й.
среда, 16 ноября 2011 г.
Максимизировать отношение
Недавно Сергей Тихонович Кузнецов загадал мне задачу.
Человек, находясь в стороне от дороги, заметил автобус. В какую точку дороги ему необходимо идти, чтобы успеть на автобус, двигаясь с как можно меньшей скоростью?
Геометрически эта задача представляется следующим образом. Прямая АС - дорога, автобус находится в точке А и движется вправо. Пешеход находится в точке В и должен направляться в некоторую току С так, чтобы отношение отрезков АС и ВС было максимальным.
При этом угол ВАС и длина отрезка АВ фиксированы, а результат зависит от величины угла АВС.
Сначала я, чисто по инерции, решил её как задачу на экстремум функции. Однако затем увидел красивое геометрическое решение, опирающееся на теорему синусов (я её специально предварительно привёл в блоге :) )
А так как синус не может превышать единицы, то нужно двигаться под прямым углом к исходном направлению на автобус.
Заметим, что решение существует лишь для острого угла между дорогой и направлением на автобус.
Человек, находясь в стороне от дороги, заметил автобус. В какую точку дороги ему необходимо идти, чтобы успеть на автобус, двигаясь с как можно меньшей скоростью?
При этом угол ВАС и длина отрезка АВ фиксированы, а результат зависит от величины угла АВС.
Сначала я, чисто по инерции, решил её как задачу на экстремум функции. Однако затем увидел красивое геометрическое решение, опирающееся на теорему синусов (я её специально предварительно привёл в блоге :) )
А так как синус не может превышать единицы, то нужно двигаться под прямым углом к исходном направлению на автобус.
Заметим, что решение существует лишь для острого угла между дорогой и направлением на автобус.
вторник, 15 ноября 2011 г.
Двумя способами
С математической точки зрения число 50 интересно тем, что это - наименьшее натуральное число, которое представляется в виде суммы двух квадратов натуральных чисел двумя способами.
50 = 49 + 1 = 25 + 25.
Если заменить слово "натуральных" словом "целых", то наименьшим числом такого рода будет 25:
25 = 16 + 9 = 0 + 25.
Оказывается есть простой способ определить, представимо ли число в виде суммы двух квадратов двумя способами. Для этого оно должно иметь в своём разложении как минимум 2 (не обязательно различных) простых множителя, дающих остаток 1 при делении на 4. А количество простых множителей, дающих остаток 3 при делении на 4 должно быть чётным.
Например, число 305 = 5 х 61. И 5 и 61 дают остаток 1 при делении на 4. Множителей, дающих остаток 3 в его разложении нет, т.е. их 0 штук - чётное число. Значит, 305 представляется в виде 305=42+172=72+162.
Зная это, подобные числа можно конструировать. Возьмём простое число 5, умножим его на простое число 13, и дважды умножим на простое число 3. Полученный результат 585 представляется как:
585=32+242=122+212.
50 = 49 + 1 = 25 + 25.
Если заменить слово "натуральных" словом "целых", то наименьшим числом такого рода будет 25:
25 = 16 + 9 = 0 + 25.
Оказывается есть простой способ определить, представимо ли число в виде суммы двух квадратов двумя способами. Для этого оно должно иметь в своём разложении как минимум 2 (не обязательно различных) простых множителя, дающих остаток 1 при делении на 4. А количество простых множителей, дающих остаток 3 при делении на 4 должно быть чётным.
Например, число 305 = 5 х 61. И 5 и 61 дают остаток 1 при делении на 4. Множителей, дающих остаток 3 в его разложении нет, т.е. их 0 штук - чётное число. Значит, 305 представляется в виде 305=42+172=72+162.
Зная это, подобные числа можно конструировать. Возьмём простое число 5, умножим его на простое число 13, и дважды умножим на простое число 3. Полученный результат 585 представляется как:
585=32+242=122+212.
понедельник, 14 ноября 2011 г.
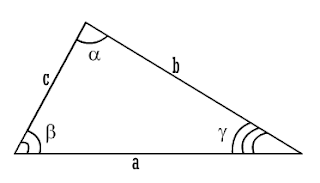
Теорема синусов
Пусть в треугольнике со сторонами a, b, c углы равны 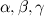
В треугольнике отношение стороны к синусу противолежащего угла будет постоянным.
Кстати, обратите внимание, как расположены углы. Традиция именования углов состоит в том, что угол и сторона, обозначаемые соответственными буквами, не являются смежными.
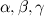
В треугольнике отношение стороны к синусу противолежащего угла будет постоянным.
Кстати, обратите внимание, как расположены углы. Традиция именования углов состоит в том, что угол и сторона, обозначаемые соответственными буквами, не являются смежными.
воскресенье, 13 ноября 2011 г.
50
Пятьдесят - это не обычное число. Пятьдесят - это необычное число.
Гарик Мартиросян в номере "Караоке" на юбилейной игре КВН.
суббота, 12 ноября 2011 г.
пятница, 11 ноября 2011 г.
четверг, 10 ноября 2011 г.
Среднее геометрическое
Ещё один способ получить среднее для нескольких чисел - это их перемножить, а затем извлечь корень такой степени, сколько чисел перемножалось.
Что же в этом геометрического? Для двух положительных чисел a, b среднее, полученное таким методом, будет равно стороне квадрата, имеющего ту же площадь, что и прямоугольник со сторонами a и b.
Среднее геометрическое называют также средним пропорциональным, и вот почему. Рассмотрим пропорцию:
По свойству пропорции, x2 = ab, т.е. x будет являться средним геометрическим (пропорциональным) чисел a и b.
Что же в этом геометрического? Для двух положительных чисел a, b среднее, полученное таким методом, будет равно стороне квадрата, имеющего ту же площадь, что и прямоугольник со сторонами a и b.
Среднее геометрическое называют также средним пропорциональным, и вот почему. Рассмотрим пропорцию:
По свойству пропорции, x2 = ab, т.е. x будет являться средним геометрическим (пропорциональным) чисел a и b.
среда, 9 ноября 2011 г.
Правильный вынос из-под корня
Стабильно в первую пятёрку самых читаемых постов блога "Десять Букв" входит заметка о правильно-неправильном выносе из-под корня. Причём люди попадают сюда просто в поисках правил выноса из-под корня. На всякий случай, чтобы не вводить читателей в заблуждение, подчеркну, что в описанном там случае мы получаем правильный результат, выполняя неправильные действия, и в общем случае равенство
в котором под корнем смешанное число, выполняться не будет. (А поиск таких значений a, b, c, при котором оно верно - задача интересная. Но я публиковал её тогда, когда у блога было мало читателей, и комментариев пока нет.)
Чтобы выполнить вынос из-под корня правильно, нужно подкоренное число представить в виде произведения чисел, одно из которых является полным квадратом. Например:
А корень из дроби является частным от деления корня из числителя на корень из знаменателя.
Любителям же математических головоломок предлагаю рассмотреть пример ещё одно неправильного выноса:
Существуют ли другие числа, для которых подобное возможно?
в котором под корнем смешанное число, выполняться не будет. (А поиск таких значений a, b, c, при котором оно верно - задача интересная. Но я публиковал её тогда, когда у блога было мало читателей, и комментариев пока нет.)
Чтобы выполнить вынос из-под корня правильно, нужно подкоренное число представить в виде произведения чисел, одно из которых является полным квадратом. Например:
А корень из дроби является частным от деления корня из числителя на корень из знаменателя.
Любителям же математических головоломок предлагаю рассмотреть пример ещё одно неправильного выноса:
Существуют ли другие числа, для которых подобное возможно?
вторник, 8 ноября 2011 г.
Средние в трапеции
Длина средней линии трапеции равна среднему арифметическому её оснований. А длина отрезка, соединяющего боковые стороны, проведённого через точку пересечения диагоналей, параллельно основаниям трапеции, равна среднему гармоническому оснований.
понедельник, 7 ноября 2011 г.
Среднее гармоническое
Решая задачу о средней скорости автобуса, мы получили значение, что находится между его наибольшей и наименьшей скоростями, но в то же время меньшее их среднего арифметического.
Выражение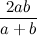 , по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.
, по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.
Сначала каждое из чисел a, b, нужно заменить его обратной величиной. Затем найти среднее арифметическое этих обратных величин:
И, наконец, снова выполнить переворот дроби, получая приведённую выше формулу.
Среднее гармоническое никогда не превышает среднего арифметического, и равно ему, если равны числа от которых оно берётся.
Выражение
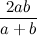 , по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.
, по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.Сначала каждое из чисел a, b, нужно заменить его обратной величиной. Затем найти среднее арифметическое этих обратных величин:
И, наконец, снова выполнить переворот дроби, получая приведённую выше формулу.
Среднее гармоническое никогда не превышает среднего арифметического, и равно ему, если равны числа от которых оно берётся.
воскресенье, 6 ноября 2011 г.
суббота, 5 ноября 2011 г.
Средняя скорость
Классическая задача, в которой автобус едет из пункта А в пункт В со скоростью 40к/ч, а возвращается со скоростью 60 км/ч, часто направляет по ложному следу школьника, которому необходимо найти среднюю скорость.
Очевидный шаг - найти среднее арифметическое скоростей "туда" и "обратно", дающий ответ 50 км/ч, является неправильным. И вот почему: двигаясь с меньшей скоростью, автобус затратит большее время на путь, следовательно, эта скорость окажет большее влияние на среднюю. Рассмотрим крайний случай: скорость "туда" равна 100 км/ч, а обратно - 0 км/ч. Среднее арифметическое этих скоростей, опять-таки, 50 км/ч, но в данном случае автобус и вовсе не прибудет в пункт А.
Чтобы правильно решать подобные задачи, необходимо вспомнить определение средней скорости. Средняя скорость является отношением всего пройденного расстояния к общему затраченному времени.
Пусть расстояние между пунктами равно s. Тогда автобус прошёл расстояние, равное 2s. Времени на путь из А в В он затратил s/40 ч, а на обратный - s/60 ч. Общее время составит:
Теперь можно находить среднюю скорость.
Очевидный шаг - найти среднее арифметическое скоростей "туда" и "обратно", дающий ответ 50 км/ч, является неправильным. И вот почему: двигаясь с меньшей скоростью, автобус затратит большее время на путь, следовательно, эта скорость окажет большее влияние на среднюю. Рассмотрим крайний случай: скорость "туда" равна 100 км/ч, а обратно - 0 км/ч. Среднее арифметическое этих скоростей, опять-таки, 50 км/ч, но в данном случае автобус и вовсе не прибудет в пункт А.
Чтобы правильно решать подобные задачи, необходимо вспомнить определение средней скорости. Средняя скорость является отношением всего пройденного расстояния к общему затраченному времени.
Пусть расстояние между пунктами равно s. Тогда автобус прошёл расстояние, равное 2s. Времени на путь из А в В он затратил s/40 ч, а на обратный - s/60 ч. Общее время составит:
Теперь можно находить среднюю скорость.
пятница, 4 ноября 2011 г.
четверг, 3 ноября 2011 г.
понедельник, 31 октября 2011 г.
Облако слов
Интересный сервис wordle.net может провести частотный анализ текстов на веб-странице и представить результаты в виде симпатичного облака слов.
Вот какой результат выдала эта система о "Десяти буквах":
Увеличив число отображаемых постов на странице я дал ссылку на блог другой системе: WordCloud
Она выдала следующее:
Здесь в облако попали также фрагменты html-кода страницы
пятница, 28 октября 2011 г.
ЗЫ
Когда я, лет 8 назад, получил регулярный доступ в интернет и начал общаться на форумах (в основном, на форуме по Цивилизации), многие слова и выражения были непонятны. Среди них было и буквосочетание "ЗЫ". Взглянув на клавиатуру я догадался, что так в рунете часто обозначают постскриптум.
А сейчас узнал интересный факт: в кабардино-черкесском языке слово зы обозначает числительное 1.
А сейчас узнал интересный факт: в кабардино-черкесском языке слово зы обозначает числительное 1.
суббота, 22 октября 2011 г.
Выпуклый и невыпуклый многогранники
Иногда из одинакового набора граней можно собрать различные многогранники: как выпуклый, так и невыпуклый. Объём какого из них в этом случае будет больше? Интуитивно кажется, что выпуклого, однако это не всегда так. Ролик с Этюдов демонстрирует, что в некоторых случаях невыпуклый многогранник будет иметь больший объём.
Для приведённого в видео примере отношение объёмов составляет 1,163... Каким же является максимально возможное отношение объёмов невыпуклого и выпуклого многогранников, составленных из одних и тех же граней, до сих пор неизвестно.
Для приведённого в видео примере отношение объёмов составляет 1,163... Каким же является максимально возможное отношение объёмов невыпуклого и выпуклого многогранников, составленных из одних и тех же граней, до сих пор неизвестно.
вторник, 18 октября 2011 г.
Десятибуквенное числительное
Когда-то я составлял список числительных из различных языков, количество букв в которых равно их значению. Это удалось сделать для чисел от 1 до 18, кроме десятки.
И вот сегодня Ali обнаружил слово Mahtlāctli, которое в ацтекском языке науатль обозначает число 10
И вот сегодня Ali обнаружил слово Mahtlāctli, которое в ацтекском языке науатль обозначает число 10
четверг, 13 октября 2011 г.
Смена системы счисления: прогресс
В задаче о поиска чисел, которые в q-ичной системе счисления записывалось бы как p, а в p-ичной - как q продвигается с помощью наших читателей.
Вадим заметил, что любое число, записываемое как n в десятичной системе счисления выглядит как 10 в системе по основанию n.
А Николай нашёл принципиально отличный пример: запись "65" в 87-ричной системе счисления означает 6 * 87 + 5 = 527. То же самое означает и запись "87" в 65-ричной системе: 8 * 65 + 7 = 527.
Задачу поиска не более чем двузначных p и q можно записать так: Пусть p состоит из цифр a и b, а q - из цифр c и d.
Тогда запись (ab)cd означает число a*cd+b=10ac+ad+b.
А запись (cd)ab означает число c*ab+d=10ac+bc+d. (Запись ab означает не произведение, а число с цифрами a и b).
Тогда получаем уравнение
ad + b = bc + d
Откуда
(a - 1)d = (c - 1)b
Получаем ещё одну группу решений: если оба числа начинаются на 1. К примеру, запись "15" в 19-ричной системе означает число 15+9=24. То же самое будет означать и запись "19" в 15-ричной системе.
Если же d=c-1, а b=a-1 (как в числах 87 и 65) - тоже равенство выполнится.
Вадим заметил, что любое число, записываемое как n в десятичной системе счисления выглядит как 10 в системе по основанию n.
А Николай нашёл принципиально отличный пример: запись "65" в 87-ричной системе счисления означает 6 * 87 + 5 = 527. То же самое означает и запись "87" в 65-ричной системе: 8 * 65 + 7 = 527.
Задачу поиска не более чем двузначных p и q можно записать так: Пусть p состоит из цифр a и b, а q - из цифр c и d.
Тогда запись (ab)cd означает число a*cd+b=10ac+ad+b.
А запись (cd)ab означает число c*ab+d=10ac+bc+d. (Запись ab означает не произведение, а число с цифрами a и b).
Тогда получаем уравнение
ad + b = bc + d
Откуда
(a - 1)d = (c - 1)b
Получаем ещё одну группу решений: если оба числа начинаются на 1. К примеру, запись "15" в 19-ричной системе означает число 15+9=24. То же самое будет означать и запись "19" в 15-ричной системе.
Если же d=c-1, а b=a-1 (как в числах 87 и 65) - тоже равенство выполнится.
понедельник, 10 октября 2011 г.
Прогрессия в дате
Вчера, девятого октября, дважды наступал момент, когда время вместе с датой формировало арифметическую прогрессию.
Это случалось 06:07:08 09.10.11 и 09.10.11 12:13:14
Почему же я не написал об этом вчера? Потому что у меня опять новый игровой проект, которым, надеюсь, скоро с вами поделюсь.
Это случалось 06:07:08 09.10.11 и 09.10.11 12:13:14
Почему же я не написал об этом вчера? Потому что у меня опять новый игровой проект, которым, надеюсь, скоро с вами поделюсь.
вторник, 4 октября 2011 г.
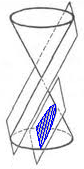
Вращение гиперкуба
Если последовательно рассмотреть точку, отрезок, квадрат и куб, можно заметить, что каждый следующий объект получается из предыдущего дублированием и параллельным и переносом копии вдоль нового измерения. Траектории переноса каждого их элемента формирует элемент более высокой размерности. Например, 4 стороны квадрата, двигаясь, создают боковые грани куба.
Так же и куб можно сдвинуть вдоль четвёртого измерения и образуется гиперкуб. И так же, как проекцию куба можно изобразить на бумаге (двумерном объекте), четырёхмерный гиперкуб можно проецировать в пространство.
Как это выглядит, показано на видео. Смотрите его так же, как стереокартинки: глаза должны сфокусироваться на некоторой точке перед экраном, чтобы оба изображения совместились.
Так же и куб можно сдвинуть вдоль четвёртого измерения и образуется гиперкуб. И так же, как проекцию куба можно изобразить на бумаге (двумерном объекте), четырёхмерный гиперкуб можно проецировать в пространство.
Как это выглядит, показано на видео. Смотрите его так же, как стереокартинки: глаза должны сфокусироваться на некоторой точке перед экраном, чтобы оба изображения совместились.
понедельник, 3 октября 2011 г.
Вырезать одним разрезом
На листе бумаги нарисован многоугольник (не обязательно выпуклый). Можно ли так согнуть лист, чтобы этот многоугольник можно было бы вырезать одним разрезом?
Оказывается, всегда ответ - да. Вот ролик иллюстрирующий пару примеров.
Для фигуры, показанной в его заставке схема сгибов будет следующей:
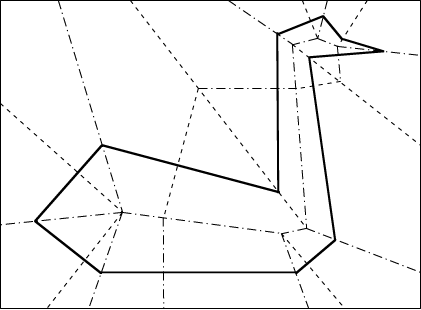
В общем виде последовательность действий для определения необходимых сгибов состоит из трёх шагов:
1. Построить прямолинейный скелет многоугольника. Как он строится иллюстрирует эта анимированная схема:
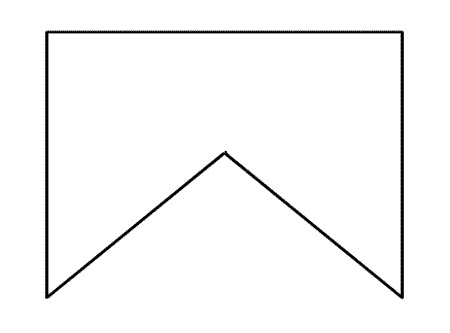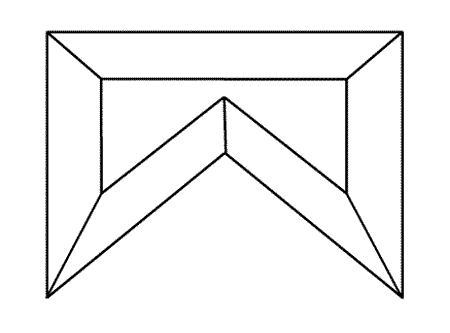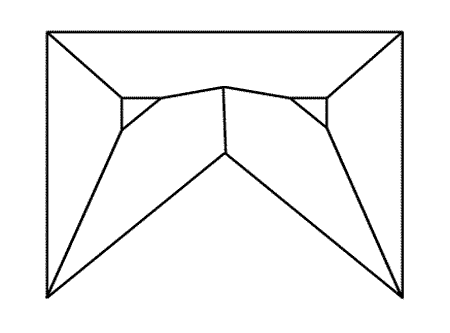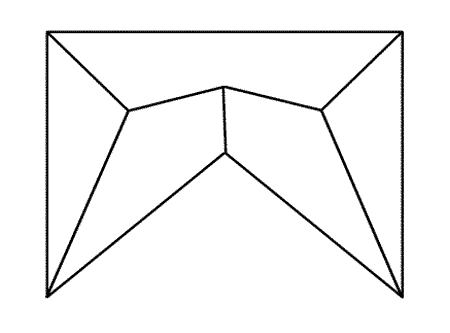
Все стороны многоугольника мы уменьшаем так, чтобы они оставались параллельны исходным положениям и все расстояния между сторонами и их начальными положениями были равными. В процессе сжатия многоугольник может разбиться на несколько областей - продолжаем уменьшение для них.
Траектории, описанные его вершинами, и будут прямолинейным скелетом.
2. Из узлов скелета опускаем перпендикуляры на те стороны, стяжкой которых эти вершины образовались.
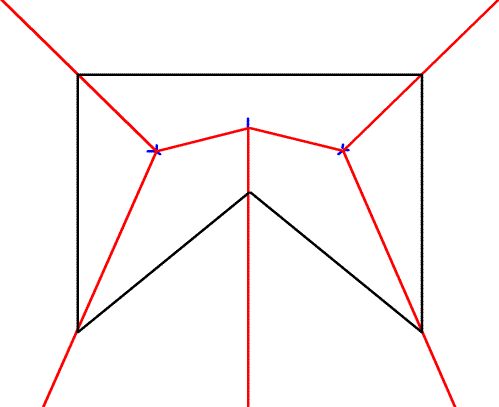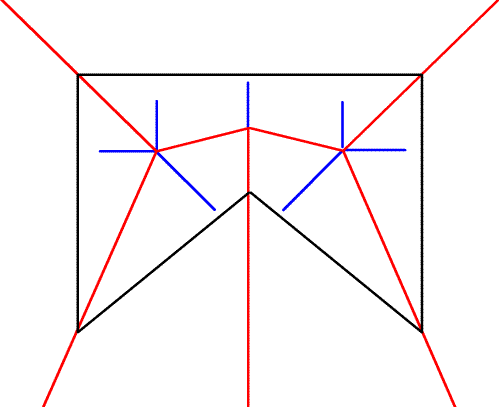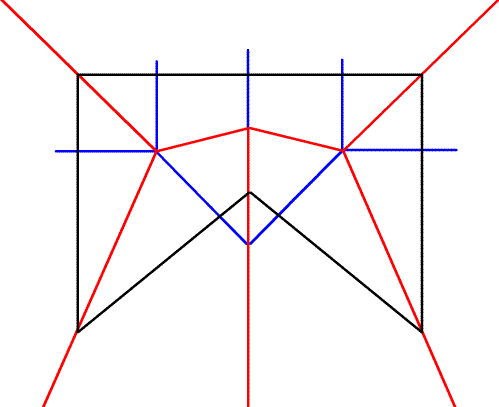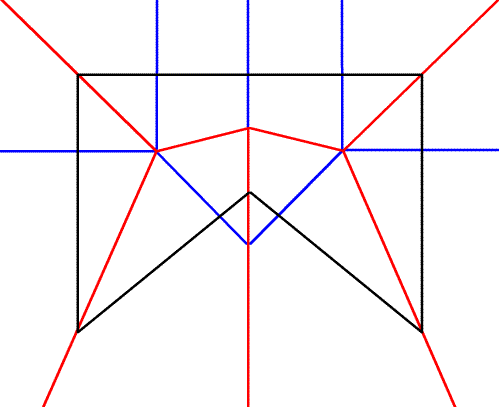
3.Определение направлений сгиба (вверх или вниз)
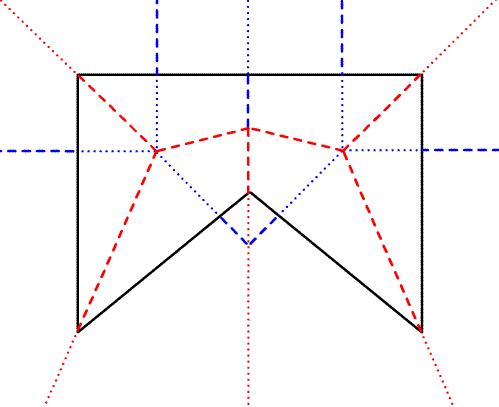
Как видите, направление меняется как только линия пересекает границу многоугольника.
Согнув лист по этой схеме, многоугольник можно будет вырезать одним разрезом.
Оказывается, всегда ответ - да. Вот ролик иллюстрирующий пару примеров.
Для фигуры, показанной в его заставке схема сгибов будет следующей:

В общем виде последовательность действий для определения необходимых сгибов состоит из трёх шагов:
1. Построить прямолинейный скелет многоугольника. Как он строится иллюстрирует эта анимированная схема:

Все стороны многоугольника мы уменьшаем так, чтобы они оставались параллельны исходным положениям и все расстояния между сторонами и их начальными положениями были равными. В процессе сжатия многоугольник может разбиться на несколько областей - продолжаем уменьшение для них.
Траектории, описанные его вершинами, и будут прямолинейным скелетом.
2. Из узлов скелета опускаем перпендикуляры на те стороны, стяжкой которых эти вершины образовались.

3.Определение направлений сгиба (вверх или вниз)

Как видите, направление меняется как только линия пересекает границу многоугольника.
Согнув лист по этой схеме, многоугольник можно будет вырезать одним разрезом.
воскресенье, 2 октября 2011 г.
Трёхмерное множество Мандельброта
Вот какую удивительную структуру удалось получить Тому Лову в 2010 году, применив формулы преобразований для трёхмерного пространства, аналогичные тем, на основе которых строится озеро Мандельброта.
суббота, 1 октября 2011 г.
Прогноз Томаса Мальтуса
В конце XVIII века английским учёным Томасом Мальтусом было выведено 2 принципа:
- население растёт в геометрической прогрессии
- ресурсы растут в арифметической прогрессии.
Поэтому рано или поздно имеющихся ресурсов не будет хватать для обеспечения потребностей растущего населения.
- население растёт в геометрической прогрессии
- ресурсы растут в арифметической прогрессии.
Поэтому рано или поздно имеющихся ресурсов не будет хватать для обеспечения потребностей растущего населения.
понедельник, 26 сентября 2011 г.
Меняем основания
(2)10 = (10)2
А есть ли ещё такие числа p и q, чтобы одной и то же число в q-ичной системе счисления записывалось бы как p, а в p-ичной - как q?
А есть ли ещё такие числа p и q, чтобы одной и то же число в q-ичной системе счисления записывалось бы как p, а в p-ичной - как q?
Турнир по Цивилизации 5 с призами от компании 1С-СофтКлаб
На моём родном форуме по Цивилизации 5 начался турнир Гран-При "На зависть птицам".

В этом турнире нам предстоит вывести Россию в космос и запустить космический корабль к Альфе Центавра. Уникальная особенность нашей страны – Богатства Сибири. Стратегические ресурсы дают +1 к производству. Держава получает лошадей, железо и уран в удвоенном размере.
Противники: Япония, Англия, Персия, Франция, Сиам, Турция, Китай и Ирокезы.
Используйте все свои умения дипломата, стратега, военачальника и аналитика, чтобы как можно скорее отправить экспедицию к звёздам. Ведь золотой, серебряный и бронзовый призеры турнира получат по золотому изданию Цивилизации 5 от 1С-СофтКлаб!
Узнать подробнее о турнире и подключиться к обсуждению можно в форуме Цив-Клуба Нашфанатики Civfanatics.ru.

В этом турнире нам предстоит вывести Россию в космос и запустить космический корабль к Альфе Центавра. Уникальная особенность нашей страны – Богатства Сибири. Стратегические ресурсы дают +1 к производству. Держава получает лошадей, железо и уран в удвоенном размере.
Противники: Япония, Англия, Персия, Франция, Сиам, Турция, Китай и Ирокезы.
Используйте все свои умения дипломата, стратега, военачальника и аналитика, чтобы как можно скорее отправить экспедицию к звёздам. Ведь золотой, серебряный и бронзовый призеры турнира получат по золотому изданию Цивилизации 5 от 1С-СофтКлаб!
Узнать подробнее о турнире и подключиться к обсуждению можно в форуме Цив-Клуба Нашфанатики Civfanatics.ru.
пятница, 23 сентября 2011 г.
Пригодилось!
Профессор встречает своего выпускника и интересуется:
- Ну как, вам в жизни пригодилась высшая математика?
- Конечно же! Помнится, однажды с меня ветром сорвало шляпу и та упала посредине лужи. Я вспомнил ваши занятия, согнул проволоку в виде интеграла и вытащил шляпу!
- Ну как, вам в жизни пригодилась высшая математика?
- Конечно же! Помнится, однажды с меня ветром сорвало шляпу и та упала посредине лужи. Я вспомнил ваши занятия, согнул проволоку в виде интеграла и вытащил шляпу!
четверг, 22 сентября 2011 г.
среда, 21 сентября 2011 г.
Умножение матриц
Матрицы можно перемножать только тогда, когда у первого множителя столько же столбцов, сколько строк у второго. Результат будет иметь столько строк, сколько первый множитель, и столько столбцов, сколько второй.
Принцип умножения можно увидеть из примера:
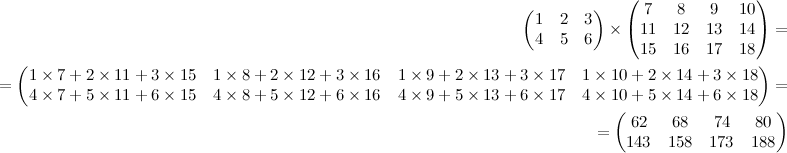
Результат умножение зависит от порядка множителей. Как видите, в данном случае при ином их порядке оно окажется вообще невозможным.
Принцип умножения можно увидеть из примера:
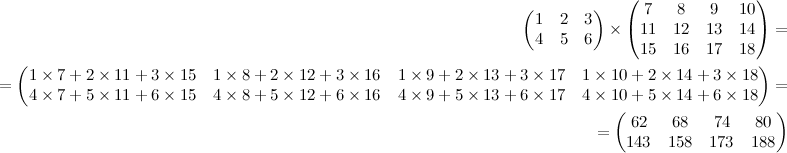
Результат умножение зависит от порядка множителей. Как видите, в данном случае при ином их порядке оно окажется вообще невозможным.
вторник, 20 сентября 2011 г.
Что такое матрицы
Сначала в школе изучаются числа и действия над ними. Затем выясняется, что существуют векторы, описываемые парой, тройкой, или, в общем случае, несколькими числами. И эти векторы также можно складывать, вычитать, и перемножать (даже целыми двумя способами).
F матрица - это объект, представляющий собой таблицу из чисел. Матрицы также можно складывать, вычитать и умножать. Складывать и вычитать можно матрицы, у которых совпадают размеры. Для этого достаточно сложить их соответстсвующие элементы.
Например,
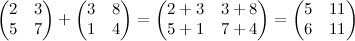
F матрица - это объект, представляющий собой таблицу из чисел. Матрицы также можно складывать, вычитать и умножать. Складывать и вычитать можно матрицы, у которых совпадают размеры. Для этого достаточно сложить их соответстсвующие элементы.
Например,
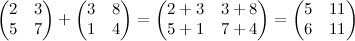
понедельник, 19 сентября 2011 г.
Коммутативность
А почему у операции возведения в степень два обратных действия, а у сложения и умножения - лишь одно? Потому, что при сложении и умножении перестановка операндов не влияет на результат. Такие операции называюьтся коммутативными. Однако с возведением не так: в общем случае 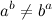
Скажем, 3^2 = 9, а 2^3 = 8. Такая операция некоммутативна.
Некоммутативным также является умножение матриц, поэтому там выделяется умножение слева и умножение мправа.
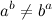
Скажем, 3^2 = 9, а 2^3 = 8. Такая операция некоммутативна.
Некоммутативным также является умножение матриц, поэтому там выделяется умножение слева и умножение мправа.
воскресенье, 18 сентября 2011 г.
Что такое логарифм
Для сложения обратным действием является вычитание (чтобы найти неизвестное слагаемое, надо из суммы вычесть изветсное). Для умножения - деление (чтобы найти неизвестный множитель, надо произведение разделить на известный).
А для возведения в степень целых два действия будут обратными: извлечение корня и логарифмирование. Если нужно узнать, какое число возвели в известную степень, из результата нужно извлечь корень этой степени.
Решением уравнения xa = b будет
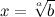
Однако же, если неизвестно, в какую степень возводили известное число, следует привлечь логарифмирование. И решением уравнения ax = b будет x = logab
Читается как "Логарифм b по основанию a." И результатом этого выражения будет такая степень, в которую нужно возвести число a (основание), чтобы получить b.
Например, log39 = 2, т. к. чтобы получить 9, 3 надо возвести в квадрат.
А log216 = 4б т. к. 24 = 14
А для возведения в степень целых два действия будут обратными: извлечение корня и логарифмирование. Если нужно узнать, какое число возвели в известную степень, из результата нужно извлечь корень этой степени.
Решением уравнения xa = b будет
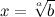
Однако же, если неизвестно, в какую степень возводили известное число, следует привлечь логарифмирование. И решением уравнения ax = b будет x = logab
Читается как "Логарифм b по основанию a." И результатом этого выражения будет такая степень, в которую нужно возвести число a (основание), чтобы получить b.
Например, log39 = 2, т. к. чтобы получить 9, 3 надо возвести в квадрат.
А log216 = 4б т. к. 24 = 14
суббота, 17 сентября 2011 г.
Хроматическое число плоскости
Если каждую точку плоскости раскрасить в один из двух цветов, то обязательно найдётся отрезок длины 1, оба конца которого имеют одинаковый цвет. Для доказательства этого достаточно рассмотреть единичную окружность. Если хотя бы одна точка на ней будет совпадать по цвету с центром, то таким отрезком будет её радиус. Если же нет - то концы искомого отрезка будут лежать на самой окружности.
Даже если раскрасить плоскость в 3 цвета, единичный отрезок с одноцветными концами найдётся.
А вот для 4, 5 и 6 цветов - неизвестно, найдётся ли такой отрезок или есть раскраска, делающая его существование невозможным.
Даже если раскрасить плоскость в 3 цвета, единичный отрезок с одноцветными концами найдётся.
А вот для 4, 5 и 6 цветов - неизвестно, найдётся ли такой отрезок или есть раскраска, делающая его существование невозможным.
пятница, 16 сентября 2011 г.
Первый замечательный предел
Первым замечательным пределом называется выражение
Оно означает, что для бесконечно малых значений аргумента синус эквивалентен самому числу. Помимо решения собственно пределов, это свойство используется в промежуточных вычислениях. Например, нам нужно вычислить синус десяти градусов. Преобразуем их в радианы (180 градусов это пи радиан, но для вычислений в уме можно просто делить на 60). Значит, синус 10 градусов - примерно одна шестая. Калькулятор даёт результат 0,1736...
Этим приёмом стоит пользоваться для углов, не превышающих 45 градусов.
Оно означает, что для бесконечно малых значений аргумента синус эквивалентен самому числу. Помимо решения собственно пределов, это свойство используется в промежуточных вычислениях. Например, нам нужно вычислить синус десяти градусов. Преобразуем их в радианы (180 градусов это пи радиан, но для вычислений в уме можно просто делить на 60). Значит, синус 10 градусов - примерно одна шестая. Калькулятор даёт результат 0,1736...
Этим приёмом стоит пользоваться для углов, не превышающих 45 градусов.
четверг, 15 сентября 2011 г.
среда, 14 сентября 2011 г.
вторник, 13 сентября 2011 г.
День программиста
С сегодняшнего дня пора бы продолжать публикацию математических постов. :)

А пока - на финишной прямой игра Save the Paintings, в которой нужно восстановить шедевры живописи, сегодня сделал прототип игровой механики нового проекта. А в блоге GameGems.OrG собираю игры, которые понравились лично мне, пишу им рецензии, а вчера даже взял интервью у разработчика одной из них.
XV тур Математического Марафона ещё идёт, подключайтесь!

А пока - на финишной прямой игра Save the Paintings, в которой нужно восстановить шедевры живописи, сегодня сделал прототип игровой механики нового проекта. А в блоге GameGems.OrG собираю игры, которые понравились лично мне, пишу им рецензии, а вчера даже взял интервью у разработчика одной из них.
XV тур Математического Марафона ещё идёт, подключайтесь!
четверг, 25 августа 2011 г.
Сумма квадратов ряда Фибоначчи
На сайте http://mathoverflow.net сейчас идёт конкурс доказательств без слов. Вот как пользователь serargus показывает, что сумма квадратов n первых членов ряда Фибоначчи равна произведению n-го на (n+1)-й член ряда.
воскресенье, 21 августа 2011 г.
Мантисса
Мантисса - это дробная часть числа. Операция взятия дробной части обозначается фигурными скобками.
{5}=0
{4,37}=0,37
По определению, дробная часть числа равна разности между числом и целой частью из него. {x}=x-[x]. Поскольку целая часть числа всегда меньше его самого, то дробная часть числа всегда положительна.
{-2,7}=0,3
{5}=0
{4,37}=0,37
По определению, дробная часть числа равна разности между числом и целой частью из него. {x}=x-[x]. Поскольку целая часть числа всегда меньше его самого, то дробная часть числа всегда положительна.
{-2,7}=0,3
суббота, 20 августа 2011 г.
Антье
Антье - это не французский математик :) Так называется целая часть числа, то есть наименьшее целое число, меньшее данного. Обозначается функция взятия целой части квадратными скобками.
[2]=2
[3,5]=3
[-5,2]=-6
[2]=2
[3,5]=3
[-5,2]=-6
пятница, 19 августа 2011 г.
пятница, 22 июля 2011 г.
Международный день числа Пи
Сегодня отмечается международный день числа пи. Дело в том, что текущая дата, записанная в виде дроби 22/7 является достаточно точным рациональным приближением этого числа. Это приближение было найдено ещё Архимедом.
А ещё сегодня три года нашему проекту "Приглашение в мир математики", где вы можете найти занимательные задачи, информацию о проведении олимпиады Кенгуру, внешнего тестирования и многое другое.
А ещё сегодня три года нашему проекту "Приглашение в мир математики", где вы можете найти занимательные задачи, информацию о проведении олимпиады Кенгуру, внешнего тестирования и многое другое.
вторник, 19 июля 2011 г.
X
Есть две версии возникновения римских цифр X (10) и V(5). По одной из них, первоначально при счёте девять палочек-единиц ставились вертикально, а десятой - перечёркивали их. Позже такая конструкция преобразовалась в одну палочку, перечёркнутую другой (X). А пятёрка V получилась как половина девятки.
По другой же версии, первичен символ пятёрки - раскрытая ладонь (V). Сложив две такие ладони, получаем десятку (X)
По другой же версии, первичен символ пятёрки - раскрытая ладонь (V). Сложив две такие ладони, получаем десятку (X)
вторник, 5 июля 2011 г.
257982
Вычёркивая всеми различными способами цифры из этого числа, можно получить 62 значения. Сложив их, получим исходное число:
2 + 8 + 82 + 9 + 92 + 98 + 982 + 7 + 72 + 78 + 782 + 79 + 792 + 798 + 7982 + 5 + 52 + 58 + 582 + 59 + 592 + 598 + 5982 + 57 + 572 + 578 + 5782 + 579 + 5792 + 5798 + 57982 + 2 + 22 + 28 + 282 + 29 + 292 + 298 + 2982 + 27 + 272 + 278 + 2782 + 279 + 2792 + 2798 + 27982 + 25 + 252 + 258 + 2582 + 259 + 2592 + 2598 + 25982 + 257 + 2572 + 2578 + 25782 + 2579 + 25792 + 25798 = 257982
Числами с такими свойствами заинтересовался Sirion с форума Назвы. Как оказалось, в Интернет-энциклопедии целочисленных последовательностей, уже есть соответствующая запись, однако Sirion'y удалось расширить представленный там список.
2 + 8 + 82 + 9 + 92 + 98 + 982 + 7 + 72 + 78 + 782 + 79 + 792 + 798 + 7982 + 5 + 52 + 58 + 582 + 59 + 592 + 598 + 5982 + 57 + 572 + 578 + 5782 + 579 + 5792 + 5798 + 57982 + 2 + 22 + 28 + 282 + 29 + 292 + 298 + 2982 + 27 + 272 + 278 + 2782 + 279 + 2792 + 2798 + 27982 + 25 + 252 + 258 + 2582 + 259 + 2592 + 2598 + 25982 + 257 + 2572 + 2578 + 25782 + 2579 + 25792 + 25798 = 257982
Числами с такими свойствами заинтересовался Sirion с форума Назвы. Как оказалось, в Интернет-энциклопедии целочисленных последовательностей, уже есть соответствующая запись, однако Sirion'y удалось расширить представленный там список.
понедельник, 4 июля 2011 г.
Приближённое устное извлечение квадратного корня
Задумавшись над вопросом, поднятом в комментарии к посту про логарифм, у меня, похоже, получилось сформулировать определённый метод (возможно, что-то я просто когда-то читал и вспомнилось).
Итак, для начала определим, сколько цифр вынесется из-под корня. Их будет вдвое меньше (с округлением в большую сторону), чем у исходного числа. Например, извлекая корень из числа 57535468, получим четырёхзначный результат.
Далее, если в исходно числе чётное число цифр, рассмотрим его первые две цифры, а если не чётное - то первую одну. Число 57 находится между двумя полными квадратами: 72=49 и 82=64. Значит, первой цифрой результата будет семёрка.
Вторую цифру найдём интерполяцией: 57 находится примерно посередине между 49 и 64, значит, корень из него будет равен примерно 7,5 и квадратный корень корень из искомого числа 57535468 составит примерно 7500. Калькулятор даёт результат 7585,2...
Итак, для начала определим, сколько цифр вынесется из-под корня. Их будет вдвое меньше (с округлением в большую сторону), чем у исходного числа. Например, извлекая корень из числа 57535468, получим четырёхзначный результат.
Далее, если в исходно числе чётное число цифр, рассмотрим его первые две цифры, а если не чётное - то первую одну. Число 57 находится между двумя полными квадратами: 72=49 и 82=64. Значит, первой цифрой результата будет семёрка.
Вторую цифру найдём интерполяцией: 57 находится примерно посередине между 49 и 64, значит, корень из него будет равен примерно 7,5 и квадратный корень корень из искомого числа 57535468 составит примерно 7500. Калькулятор даёт результат 7585,2...
четверг, 30 июня 2011 г.
Находим логарифм.
Целая часть десятичного логарифма числа на 1 меньше количества его цифр. А чтобы найти первый знак мантиссы, наш читатель рекомендует прибавить 2 к первой цифре числа, от которого берётся логарифм. Разумеется, кроме случаев, когда логарифм извлекают из числа, начинающегося на 8 (тогда мантиса будет равна 9) или на 9 (тогда более точный результат получим, взяв за ответ количество цифр).
Например: lg(354584) = 5,5. Первую пятёрку получили, как количество цифр минус один, а вторую - как первую цифру плюс два. Калькулятор даёт такой же результат.
Например: lg(354584) = 5,5. Первую пятёрку получили, как количество цифр минус один, а вторую - как первую цифру плюс два. Калькулятор даёт такой же результат.
среда, 29 июня 2011 г.
Цифровой корень
Возьмём натуральное число. Найдём сумму его цифр. У результата также найдём сумму цифр, и так до тех пор, пока не получится однозначное число. Полученный результат называется цифровым корнем числа.
К примеру, цифровой корень числа 123456 равен трём:
1+2+3+4+5+6=21
2+1=3
Цифровой корень для числа, записанного в десятичной системе счисления, равен остатку от деления его на 9.
К примеру, цифровой корень числа 123456 равен трём:
1+2+3+4+5+6=21
2+1=3
Цифровой корень для числа, записанного в десятичной системе счисления, равен остатку от деления его на 9.
понедельник, 27 июня 2011 г.
I Wanna Win! - Релиз!
 Наконец-то я зарелизил свою новую флеш-игру игру - I Wanna Win!
Наконец-то я зарелизил свою новую флеш-игру игру - I Wanna Win!В принципе, всё было готово в конце апреля, но то одно, то другое - уже и треть лета прошла.
В игре 25 уровней, в каждом - своя миниигра на меткость, внимание, память, логику. Сейчас игра доступна по ссылке, а через неделю пойду бороться за приз от крупных порталов.
понедельник, 30 мая 2011 г.
воскресенье, 29 мая 2011 г.
среда, 25 мая 2011 г.
Подписаться на:
Сообщения (Atom)
Популярные сообщения
-
Если вы хотите проверить, содержится ли ваш телефон, год рождения или номер дома среди уже вычисленных знаков числа пи, воспользуйтесь этой ...
-
Как рассказал наш читатель в комментарии к посту о целочисленном треугольнике , площадь четырёхугольника, вписанного в окружность, вычисляе...
-
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат...
-
Приведённые квадратные уравнения легко решать по теореме Виета. Достаточно найти два числа такие, произведение которых равно свободному член...
-
Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существуе...
-
Мы привыкли доверять в расчётах компьютеру. Но иногда - чересчур полагаемся на него. А сейчас я покажу один поучительный пример, позволяющи...
-
Для числа 12 на математических часах я выбрал одну их наиболее парадоксальных формул, согласно которой сумма всего бесконечного множества на...
-
Мантисса - это дробная часть числа. Операция взятия дробной части обозначается фигурными скобками. {5}=0 {4,37}=0,37 По определению, дро...
-
Стабильно в первую пятёрку самых читаемых постов блога "Десять Букв" входит заметка о правильно-неправильном выносе из-под корня ...
-
Площадь треугольника, зная его стороны, можно найти по формуле Герона. < Где a, b, c - стороны треугольника, а p - полупериметр. Для...
Темы
число
цифра
простые
геометрия
юмор
дроби
язык
степень
делимость
пи
методы
история
квадрат
самоописывающее
время
задача
система счисления
узор
корень
тригонометрия
структура
е
сайты
конструкция
формулы
игра
факториал
функции
приближение
программа
фрактал
комбинаторика
последовательность
график
память
логарифм
вероятность
палиндром
пределы
конкурс
треугольник
магический квадрат
неизвестное
правильно-неправильное действие
видео
интеграл
уравнение
комплексные
софизм
заблуждения
процесс
ряды
цитаты
книги
окружность
прогрессия
среднее
стереометрия
число фи
выражения
графы
матрица
проценты
разрезания
логика
парабола
символ
статистика
2014
Фибоначчи
клеточный автомат
кривая
производная
фокус
головоломка
действия
иллюзия
куб
шахматы
многоугольник
новости
оказывается
оригами
подобие
построение
сложение
термин
тетраэдр
топология




.PNG/224px-Pythagorean_graphic_(2).PNG)