Интересные числа, занимательные математические факты и удивительные конструкции. Узнавайте каждый день что-то новое!
Подписаться на:
Комментарии к сообщению (Atom)
Популярные сообщения
-
Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существуе...
-
Если вы хотите проверить, содержится ли ваш телефон, год рождения или номер дома среди уже вычисленных знаков числа пи, воспользуйтесь этой ...
-
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат...
-
Важными статистическими свойствами выборки (набора чисел) являются среднее значение и медиана. Они не тождественны. Среднее значение - это ...
-
Приведённые квадратные уравнения легко решать по теореме Виета. Достаточно найти два числа такие, произведение которых равно свободному член...
-
Как рассказал наш читатель в комментарии к посту о целочисленном треугольнике , площадь четырёхугольника, вписанного в окружность, вычисляе...
-
Мантисса - это дробная часть числа. Операция взятия дробной части обозначается фигурными скобками. {5}=0 {4,37}=0,37 По определению, дро...
-
Для числа 12 на математических часах я выбрал одну их наиболее парадоксальных формул, согласно которой сумма всего бесконечного множества на...
-
Эта фраза помогает запомнить 5 знаков числа пи: соответствующие цифры равны количеству букв в словах. Что (3) я (1) знаю (4) о (1) кругах ...
-
Как мне напомнил читатель , число 1444 имеет ещё одно интересное свойство. Дело в том, что квадрат натурального числа не может оканчиваться ...
Темы
число
цифра
простые
геометрия
юмор
дроби
язык
степень
делимость
пи
методы
история
квадрат
самоописывающее
время
задача
система счисления
узор
корень
тригонометрия
структура
е
сайты
конструкция
формулы
игра
факториал
функции
приближение
программа
фрактал
комбинаторика
последовательность
график
память
логарифм
вероятность
палиндром
пределы
конкурс
треугольник
магический квадрат
неизвестное
правильно-неправильное действие
видео
интеграл
уравнение
комплексные
софизм
заблуждения
процесс
ряды
цитаты
книги
окружность
прогрессия
среднее
стереометрия
число фи
выражения
графы
матрица
проценты
разрезания
логика
парабола
символ
статистика
2014
Фибоначчи
клеточный автомат
кривая
производная
фокус
головоломка
действия
иллюзия
куб
шахматы
многоугольник
новости
оказывается
оригами
подобие
построение
сложение
термин
тетраэдр
топология
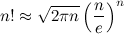


По ней же можно находить факториал от нецелых чисел. Иногда так можно запутать студентов, которые найдут 3! или 4!, а вот 3,5! как найти не знают.
ОтветитьУдалитьКстати, один из моих инженерных калькуляторов ругается на подобную запись (3,12!) и не считает, а второй безропотно выдаёт результат.
Да-да, точно, напишу об этом обязательно. Я в школе задумывался, как расширить факториал на нецелые числа, решил для несократимой дроби p/q считать произведение от 1/q до p/q, т.е. p!/q^p
ОтветитьУдалитьПравда, такая функция не была возрастающей.