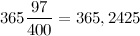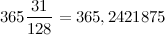Мелодия числа пи

В этом видео, наверное, самый правильный подход к представлению того, как может звучать число пи. Чтобы поставить в соответстсвие бесконечной последовталеьности цифр числа пи бесконечную последовательность звуков, применили следующий приём.

В западной музыкальной традиции в октаве 12 полутонов (если считать и белые и чёрные клавиши на фортепиано). Поэтому для начала представим чсило пи в двенадцатеричной системе счисления. Выглядеть оно будет вот так:

3.184809493B918664573A...

В двенадцатеричной системе используются цифры 0123456789AB, а цифры после запятой показывают не десятые, сотые, тысячные, а двенадцатые, сто сорок четвёртые, тысяча семьсот двадцать восьмые и т.д.

В следующем видео показано, как будет звучать эта последовательность нот.

Для благозвучия исполнитель дал нотам разную длительность, а также вместо отдельных нот стал играть аккордами, но мелодия от этого только выиграла. Любителю математики её можно поставить на телефон :)

С днём числа пи вас!

Ещё о правильно-неправильном сокращении дробей

Если сокращать дроби, зачёркивая одинаковые цифры, иногда можно получить правильный результат. Нашими читателями было найдено больше дробей с такими свойствами.

Оказывается все дроби с трёхзначными числителями и знаменателями, которые полностью сократятся при вычёркивании одинаковых цифр, есть в работе Boas, 1979 года.

Например: $\frac{124}{217} = \frac{4}{7}$, $\frac{316}{632} = \frac{1}{2}$. За полным списокм можете заглянуть по ссылке, а можете поискать самостоятельно.

А для программистов также будет интересно, что в 16-ричной системе подобных дробей с двузначными числителями и знаменателями целых 7, а не 4, как десятеричной.

Внимание. Ведущий блога не несёт ответственности, в случае, если читатели на контрольной по математике начнут сокращать так любые дроби. Например, $\frac{13}{39}$ не будет равняться $\frac{1}{9}$

Трёхзначное число

Некоторое трёхначное число записали в обратном порядке, а затем вычли из большего меньшее. В результате оказалось, что разность состоит из тех же цифр, что и исходное число.

В десятичной системе счисления ответ на задачу единственен. А в какой системе счисления есть два трёхзначных числа, удовлетворяющих условию задачи?

Злые числа

Если сложив от первой до некоторой n-й цифры дробной части числа x можно получить репдигит 666, то число x называют злым. Оказывается, злыми являются число пи и константа золотого сечения число фи. Требуемая сумма получается при складывании первых 144 или 146 цифр, соответственно.

Такое определение опять зависимо от выбранной системы счисления (кстати, в двоичной системе все иррациональные числа будут злыми). Но если рассмотреть аналогичным образом разложение числа в цепную дробь, от выбранной системы независящее, то и тут число пи окажется злым! Сумма первых 56 звеньев его цепной дроби даст 666.

Экономные числа

Разложим натуральное число на простые множители. Запись его разложения может иметь как больше цифр, чем само число (например, 2013 = 3*11*61), столько же цифр (27 = 3³) или даже быть короче (1701 = 3⁷*7 )

Числа первого вида в занимательной математике называются избыточными (wasteful). Это уже третье определение избыточного числа (первое относится к базовому свойству числа - сумме делителей, а второе - к названию числа в определённом языке).

Числа, разбиение которых на простые множители использует (с учётом больших единицы показателей степеней) столько же цифр, сколько их в самом числе, называются равноциферными (equidigital). В частности, все простые числа - равноциферны в любой системе счисления.

А те же числа, факторизация которых имеет меньше цифр, чем само число, называются экономными (economical). Наименьшее экономное число для десятичной системы - это 125 = 5³. Затем идут 128 = 2⁷ и 243 = 7³

 

Репдигит

Репдигит - это число, которое состоит из повторяющихся цифр. Например, 111 или 5555. Иногда к репдигитам относят и однозначные числа: 1, 2, ... 9.

Поскольку здесь мы имеем дело с цифрами, то в разных системах счисления разные числа окажутся репдигитами. Например, число 26 будет репдигитом в троичной системе, ведь там оно выглядит как 222.

Репдигитом в тринадцатеричной системе счисления является число 2013. А некоторые числа являются репдигитами в нескольких системах. Сразу заметим, что любое число n записывается как 11 в системе счисления с основанием n-1 и является однозначным в системах с основанием n+1 и более.

Если рассматривать только системы счисления с основанием менее n-1, первым нетривиальным множественным репдигитом будет число 15. В двоичной системе оно запишется как 1111, а в четверичной - как 33.

Следующее - число 24:
(24)₁₀ = (44)₅ = (44)₅ = (33)₇ = (22)₁₁

Три системы

Запишем число 2013 в двоичной системе:
(2013)₁₀=(11111011101)₂

В троичной:
(2013)₁₀=(2202120)₃

И в пятеричной:
(2013)₁₀=(31023)₅

Так вот, во всех этих трёх представлениях суммы цифр одинаковы!

1 + 1 + 1 + 1 + 1 + 0 + 1 + 1 + 1 + 0 + 1 =  2 + 2 + 0 + 2 + 1 + 2 + 0 = 3 + 1 + 0 + 2 + 3

Тринадцатеричная система

2013 = 11 х 13² + 11 х 13 + 11
Поэтому в тринадцатеричной системе число записывается как (BBB)₁₃

В системе счисления по основанию 13 цифры А, В, С обозначают десятичные числа 10, 11 и 12.

Нормально ли число пи?

В день числа пи в сети нередко появляются публикации со следующим утверждением. Так как число пи иррационально, то в нем нет перидода. А это значит, что любая наперед заданная последовательность цифр (к примеру, ваш номер телефона, или текст этой статьи в двоичном формате), в нем обязательно встретися. Как встретятся и зашифрованные тексты неизданных книг и описания событий будущего. Далее идет тезис о мистике числа (как-то даже мне попался пассаж о том, что "число пи, единственное разумное число во вселенной, управляет нашим миром). :D

На самом деле из тезиса об иррациональности (и даже о трансцендентности, интересно, авторы подобных "сенсационных" статей различают эти два понятия?) числа пи ничего подобного не следует. За структуру цифровой записи дробной части числа отвечает еще одна характеристика, называется она нормальность, или, точнее, нормальностью по основанию n.

Число называется n-нормальным, если в системе счисления по основанию n любая из его цифр встречается с частотой 1/n, любая последовательность из двух рядом стоящих цифр - с частотой 1/n² , из трех - 1/n³ и так далее. Для числа пи (как и для е, корня из двух, логарифма натурального двух) неизвестно не только, является ли оно нормальным по какому-либо основанию, но и то, все ли цифры встречаются в десятичном представлении его дробной части бесконечное число раз.

Високосный год

В григорианском календаре год является високосным, если его номер делится на 400 или делится на 4, но не делится на 100. Таким образом, за 400 лет будет 97 високосных годов. Таким образом, в среднем в суток в году будет
 

Однако, это неоптимальное приближение. Сейчас средняя длина тропического года, т.е. время от одного весеннего равноденствия до следующего, составляет 365,2421897. Очень хорошо приближает это значение дробь


Если строить календарь, основываясь на ней, високосными годами были бы только те, номера каких делятся на 4 и не делятся на 128. Если бы мы пользовались двоичной системой, переход на данное правило не вызвал бы проблем :)

Ещё способ

Ещё один простой способ генерации кода Грея связан со следующим процессом:

Начинаем с буквы А. Далее поступаем по следующем правилу: приписываем справа следующую букву, а после неё - повторяем все ранее записанные символы. После первого шага получим строку
АВА
После второго: АВАСАВА
После третьего:
АВАСАВАDАВАСАВА

Теперь возьмём двоичное число 0000 и обозначим его цифры как DCBA. Пробежимся по строке и будем менять на противоположную ту цифру, которая соответствует текущему символу в строке:
А: 0001
В: 0011
А: 0010
С: 0110
А: 0111
В: 0101
А: 0100
D: 1100
А: 1101
В: 1111
А: 1110
С: 1010
А: 1011
В: 1001
А: 1000

Как отметил наш читатель Вадим, есть ещё один рекурсивный способ: сначала получаем код Грея длины 3, записываем его сначала в прямом порядке, а потом в обратном. И дописываем перед первой половиной 0, а перед второй — 1.

Код Грея

Рассмотрим все возможные комбинации из трёх цифр: нулей или единиц. Обычно из записывают в таком порядке:
000
001
010
011
100
101
110
111

То есть в виде двоичных представлений числе от 0 до 7. Однако эти 8 строки можно записать и так, чтобы каждая пара соседних элементов отличалась только одним символом:
000
001
011
010
110
111
101
100

Такое упорядочивание называется кодом Грея. Заметим, что первая срока от последней также отличается ровно одним символом.

Можно ли подобное сделать для шестнадцати строк от 0000 до 1111? Да, и вот какой способ формирования 4-битного кода Грея показал мне Кузнецов Сергей Тихонович.

Обозначим 4 двоичных цифры буквами A, B, C, D. А каждое из 16 чисел будет представлено ячейкой вот в такой таблице:

Если ячейка находится в колонке (строке), отмеченной буквой, в соответствующем разряде числа будет стоять единица. Иначе - ноль.

При такой разметке таблицы числа, стоящие в соседних ячейках, будут отличаться только одним разрядом. Поэтому код Грея можно сформировать, обойдя все ячейки, например, так:

Этот путь даст нам последовательность:
1100
1110
0110
0100
0101
0001
0000
0010
0011
0111
1111
1011
1010
1000
1001
1101

Её тоже можно зациклить и начинать с любого элемента.

Троичная система

Т.к. все цифры в записи числа 2012 меньше трёх, то его можно рассмотреть как запись некоторого числа в троичной системе. Таким числом будет 2x3³+0x3²+1x3¹+2x3⁰=54+3+2=59.

Кстати, простое число 59 является решением одного из вариантов задачи о раскладывании предметов:
Торговка пыталась разложить яйца поровну в 2, 3, 4, 5 или 6 корзин, но каждый раз оставались лишними 1, 2, 3, 4 или 5 яиц, соответственно. Найдите их наименьшее возможное количество.

А каким бы был ответ задачи, если бы при таком раскладывании всегда оставалось одно лишнее яйцо и корзины бы не оказывались пустыми?

Нули и единицы

Оказывается, существует ровно 2012 последовательностей из 12 нулей и единиц, в которых группа цифр 001 встречается только 1 раз.

Также в 2012 последовательностях из 12 нулей и единиц будут равное число раз встречаться группы 0001 и 0100.

А если рассмотреть последовательности длины 13, то в 2012 из них не найдётся ни 0001, ни 0011.

Календарь-додекаэдр

На Хабрахабре passerby опубликовал ссылку на свой генератор календарей. Этот генератор может составлять календари в различных системах счисления, а также располагать их как на обычных прямоугольных листах, так и на развёртках многогранников.

Смена системы счисления: прогресс

В задаче о поиска чисел, которые в q-ичной системе счисления записывалось бы как p, а в p-ичной - как q продвигается с помощью наших читателей.

Вадим заметил, что любое число, записываемое как n в десятичной системе счисления выглядит как 10 в системе по основанию n. 

А Николай нашёл принципиально отличный пример: запись "65" в 87-ричной системе счисления означает 6 * 87 + 5 = 527. То же самое означает и запись "87" в 65-ричной системе: 8 * 65 + 7 = 527.


Задачу поиска не более чем двузначных p и q можно записать так: Пусть p состоит из цифр a и b, а q - из цифр c и d.
Тогда запись (ab)_cd означает число a*cd+b=10ac+ad+b.
А запись (cd)_ab означает число c*ab+d=10ac+bc+d. (Запись ab означает не произведение, а число с цифрами a и b).


Тогда получаем уравнение
ad + b = bc + d
Откуда
(a - 1)d = (c - 1)b


Получаем ещё одну группу решений: если оба числа начинаются на 1. К примеру, запись "15" в 19-ричной системе означает число 15+9=24. То же самое будет означать и запись "19" в 15-ричной системе.


Если же d=c-1, а b=a-1 (как в числах 87 и 65) - тоже равенство выполнится.

Меняем основания

(2)₁₀ = (10)₂

А есть ли ещё такие числа p и q, чтобы одной и то же число в q-ичной системе счисления записывалось бы как p, а в p-ичной - как q?

Шкала

Оцените по шкале от 1 до 10, насколько вероятно то, что этот вопрос использует двоичную систему счисления.

(увидел на xkcd)

X

Есть две версии возникновения римских цифр X (10) и V(5). По одной из них, первоначально при счёте девять палочек-единиц ставились вертикально, а десятой - перечёркивали их. Позже такая конструкция преобразовалась в одну палочку, перечёркнутую другой (X). А пятёрка V получилась как половина девятки.

По другой же версии, первичен символ пятёрки - раскрытая ладонь (V). Сложив две такие ладони, получаем десятку (X)

Цифровой корень

Возьмём натуральное число. Найдём сумму его цифр. У результата также найдём сумму цифр, и так до тех пор, пока не получится однозначное число. Полученный результат называется цифровым корнем числа.

К примеру, цифровой корень числа 123456 равен трём:
1+2+3+4+5+6=21
2+1=3

Цифровой корень для числа, записанного в десятичной системе счисления, равен остатку от деления его на 9.