Используя свойство медианты, можно находить рациональные приближения чисел. Покажем это на примере числа е .
Число е находится между двумя целыми числами:
2 < e < 3
Запишем границы в виде дробей:
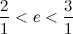
Теперь сравним е с медиантой границ:
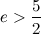
Значит, левую границу можно подвинуть:
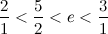
Следующее сравнение с новой медиантой:
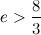
Снова уточняем оценку:
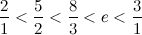
И продолжаем сравнивать число е с медиантой новый границ. В зависимости от результат сравнения будем пододвигать левую или правую границы:
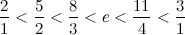
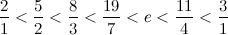
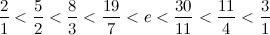
Дальше буду писать только по одной границе для компактности:
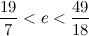
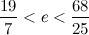
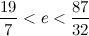
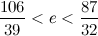
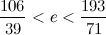
Последнее приближение отличается от е всего на две стотысячных.
Взглянем на сам процесс приближения числа е через медианты внимательнее. Подсчитаем, сколько шагов проходило до того, как новая медианта оказывалась с другой стороны от числа. Получим: 1 дробь справа (e < 3), 2 дроби слева, 1 дробь справа, 1 дробь - слева, 4 дроби справа, 1 дробь - слева, 1 дробь - справа.
Но ведь это звенья разложения дробной части числа е в цепную дробь! [1, 2, 1, 1, 4, 1, 1 ...]
Вот и ещё один алгоритм разложения числа в цепную дробь, имеющий намного больший запас точности, чем периодическая замена дробной части числа обратной величиной.
Число е находится между двумя целыми числами:
2 < e < 3
Запишем границы в виде дробей:
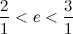
Теперь сравним е с медиантой границ:
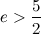
Значит, левую границу можно подвинуть:
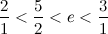
Следующее сравнение с новой медиантой:
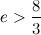
Снова уточняем оценку:
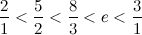
И продолжаем сравнивать число е с медиантой новый границ. В зависимости от результат сравнения будем пододвигать левую или правую границы:
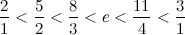
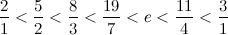
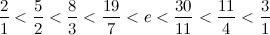
Дальше буду писать только по одной границе для компактности:
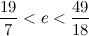
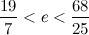
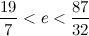
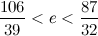
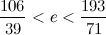
Последнее приближение отличается от е всего на две стотысячных.
Взглянем на сам процесс приближения числа е через медианты внимательнее. Подсчитаем, сколько шагов проходило до того, как новая медианта оказывалась с другой стороны от числа. Получим: 1 дробь справа (e < 3), 2 дроби слева, 1 дробь справа, 1 дробь - слева, 4 дроби справа, 1 дробь - слева, 1 дробь - справа.
Но ведь это звенья разложения дробной части числа е в цепную дробь! [1, 2, 1, 1, 4, 1, 1 ...]
Вот и ещё один алгоритм разложения числа в цепную дробь, имеющий намного больший запас точности, чем периодическая замена дробной части числа обратной величиной.


Комментариев нет:
Отправить комментарий