Решая задачу о средней скорости автобуса, мы получили значение, что находится между его наибольшей и наименьшей скоростями, но в то же время меньшее их среднего арифметического.
Выражение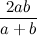 , по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.
, по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.
Сначала каждое из чисел a, b, нужно заменить его обратной величиной. Затем найти среднее арифметическое этих обратных величин:
И, наконец, снова выполнить переворот дроби, получая приведённую выше формулу.
Среднее гармоническое никогда не превышает среднего арифметического, и равно ему, если равны числа от которых оно берётся.
Выражение
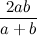 , по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.
, по которому она была найдена, называется средним гармоническим чисел a и b. Глядя на формулу, не очевидно, что она даст некоторое число между a и b, однако это так. Здесь просто совмещены несколько шагов, которые нужно сделать, чтобы найти среднее гармоническое.Сначала каждое из чисел a, b, нужно заменить его обратной величиной. Затем найти среднее арифметическое этих обратных величин:
И, наконец, снова выполнить переворот дроби, получая приведённую выше формулу.
Среднее гармоническое никогда не превышает среднего арифметического, и равно ему, если равны числа от которых оно берётся.
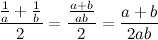


Комментариев нет:
Отправить комментарий