Периодические цепные дроби получаются только из иррациональных чисел, являющихся корнями квадратного уравнения. Для всех остальных иррациональных чисел периода в цепочке не будет.
Вот, например:
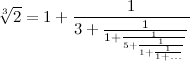
Или, в более компактном виде, это выглядит как:
[1; 3, 1, 5, 1, 1, 4, 1, 1, 8, 1, 14, 1, 10, 2, 1, 4, 12, 2, 3, 2, 1, 3, 4, 1, 1, 2, ...]
Но и среди непериодических цепных дробей встречаются имеющие красивые закономерности. Классический пример - число е, разложение которого - последовательные чётные числа, разделённые парами единиц.
[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, ...]
Вот, например:
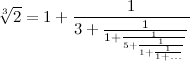
Или, в более компактном виде, это выглядит как:
[1; 3, 1, 5, 1, 1, 4, 1, 1, 8, 1, 14, 1, 10, 2, 1, 4, 12, 2, 3, 2, 1, 3, 4, 1, 1, 2, ...]
Но и среди непериодических цепных дробей встречаются имеющие красивые закономерности. Классический пример - число е, разложение которого - последовательные чётные числа, разделённые парами единиц.
[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, ...]


А вот про число e оказалось интересно. Хороший алгоритм :) Можно при изучении программирования давать как базовые задания новичкам
ОтветитьУдалить