Исследователь интересных числовых закономерностей и читатель нашего блога Николай нашёл дроби с трёхзначными числами в числителе и знаменателе, и которые тоже не меняются при вычёркивании одинаковых цифр.
Вот они:
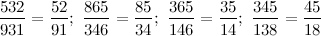
Интересные числа, занимательные математические факты и удивительные конструкции. Узнавайте каждый день что-то новое!
Может, реально есть круг случаев, подчинённых какой-то закономерности, в которых это правило применимо? Тогда есть задача их найти и обосновать теоретически.
ОтветитьУдалитьВозможно, но это ведь ещё от системы счисления будет зависеть...
ОтветитьУдалитьВозьмем цифры А, В, С, D такие, что S = А+В = С+D < 10
ОтветитьУдалитьТогда АВ * 1111 = АSSSВ
Также СD * 1111 = СSSSD
И в итоге АSSSВ / СSSSD = АВ / СD
Понятно, что единиц может быть сколько угодно
-----------------------------------------------
Пример, 5772/3774 = 572/374 = 52/34
Гениально!
ОтветитьУдалить