V

По одной из версий, римская цифра 5 - V - это полураскрытая ладонь. Тогда десятка X - это две ладони.

По другой же версии, сначала появилось обозначение для десятки. При счёте до девяти писали рядом несколько вертикальных палочек, а десятой их перечёркивали. Такой способ записи дал обозначение для десятки - перечёркнутая палочка. А пятерка - это половина десятки.

3

Это единственное натуральное число, равное сумме всех натуральных чисел, меньших себя самого

На лекции

Профессор математики ведёт лекцию. В аудитории сидят всего три студента.
Вдруг пятеро студентов выходят из аудитории. Профессор расстраивается:
- Ну вот, сейчас двое придут, и вообще никого не останется...

1681

Решая задачу, которую мне загадал Илья с форума smekalka.pp.ru, я выяснил, что число 1681 - наибольший точный квадрат, не делящийся на 100, остающийся таковым после отбрасывания последней пары цифр.

Самоописывающее равенство

5+3+2+1+0+1+0+0+0+0=12

В этом равенстве 5 нулей, 3 единицы, 2 двойки, 1 тройка, 0 четвёрок, 1 пятёрка, 0 шестёрок, 0 семёрок, 0 восьмёрок и 0 девяток. Всего в нём 12 цифр.

Приближение числа пи

Очень хороши приближением числа пи служит дробь 



Она отличается от самого числа лишь в седьмом знаке после запятой.

Запомнить эту дробь очень просто. Выпишем по два раза первые 3 нечётных числа:

1 1 3 3 5 5

Затем разобьём их на две группы:

1 1 3 | 3 5 5

Теперь правая группа идёт в числитель, а левая - в знаменатель дроби.

Пирамида квадратов

49=7²

4489=67²

444889=667²

44448889=6667²

4444488889=66667²

444444888889=666667²

так можно продолжать бесконечно

Крестики-Нолики

Автор: Мартин Гарднер.

Книга содержит эссе, задачи и головоломки из различных областей математики. Рассчитана на любителей занимательной математики.

Эту книгу мне на первом курсе дал почитать друг, а я её так и не вернул. (Нет, не думайте ничего плохого, он в курсе, что эта книга у меня и разрешает подержать её подольше :) )

В этой книге можно прочитать о:

• геометрических и алгебраических софизмах,
• задачах по теории вероятности (в частности, задача о картах со второй интернет-олимпиады по математике - оттуда),
• нерешённых математических проблемах,
• самоописывающих фразах,
• математических парадоксах,
• клеточных автоматах и игре "Жизнь"

и многом другом. К примеру, есть подборка коротких красивых логических задач.

Книгу можно скачать из библиотеки Куб.ру

Какие ещё книги по математике стоит прочитать

Лемниската

Лемниската - это геометрическое место точек, произведение расстояний от которых до фокусов - величина постоянная.

В зависимости от значения этого произведения, лемниската с двумя фокусами может представлять собой овал, восьмёрку или два яйцевидных овала.

"Восьмёрка" возникает, когда расстояние между фокусами вдвое требуемого произведения расстояний до них, с. Она описывается уравнением:



Фокусов может быть сколько угодно. Вот пример семейства лемнискат с восемью фокусами:

Эвольвента

Поставим на стол вертикально катушку ниток, и к концу нитки прикрепим грифель карандаша. Если теперь разматывать катушку в горизонтальной плоскости, держа нить всё время натянутой, карандаш нарисует эвольвенту окружности.


(Картинка с Wikipedia.org)


Хотя получившаяся кривая похожа на спираль Архимеда, это не она. Эвольвента окружности описывается уравнениями:

x=R(cosT+TsinT)
y=R(sinT-TcosT)

Гипербола

Наиболее частый пример гиперболы - график функции .

Однако такая же гипербола, только повёрнутая на 45^o будет графиком функции

Циклоида

Циклоида - это траектория точки обода катящегося колеса.


(картинка с wikipedia.org)

Она задаётся параметрически по формулам:

x = t − sint
y = 1 − cost

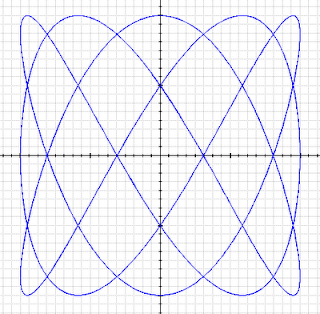
Неделя графиков продолжается!

В общем виде такой график получается по формулам
x=cos(AT)
y=sin(BT)

В данном случае A=3, B=5.
Обратите внимание, что при взаимно простых А и В кривая имеет А точек касания с вертикальной и В - с горизонтальной касательными.

Спираль Архимеда

Спираль Архимеда можно представить как траекторию жука, бегущего вдоль минутной стрелки часов.

Она строится в полярных координатах по формуле
 

Или параметрически как
x=TcosT
y=TsinT

Цветик-семицветик

Вот такой цветочек является графиком параметрически заданной функции

x:=R₁(1+cos(7T))cos(O₁T)+R₂cos(O₂T);
y:=R₁(1+cos(7T))sin(O₁T)+R₂sin(O₂T);

R₁=100,
R₂=25,
O₁=1,
O₂=500,

32

логарифм десятичный ста дециллионов

Действительно, т.к. дециллион - это 10³⁰, то lg10³²=32

18

три раза по шесть букв = шесть раз по три буквы = восемнадцать знаков

Автор: Валерий Силиванов

29

корень из восьмиста сорока одного

Действительно, ведь 29²=841

13

sek140675 с nazva.net нашёл также, что ровно тринадцать букв во фразе

чертова дюжина

Число букв равно модулю

В числах
минус пятнадцать
и
минус шестнадцать

(sek140675, nazva.net)

Два в кубе

= 8

Нашёл sek140675 с nazva.net

Неделя самоописывающих выражений

В ходе поиска десятибуквенного числительного, обозначающего в некотором языке число 10, были найдены интересные самоописывающие выражения.
То, что ровно десять букв содержится во фразе "плюс десять" заметила Наталия Макарова, исследователь магических квадратов.

Синус-косинус

Построение этого алгебраического фрактала происходит, основываясь на итерационном правиле

Z_n+1=sin(Z_n)*cos(С)

IFS-фрактал

Правило 1
x_n+1= 0.25x_n-0.13125y_n+0.325
y_n+1= 0.29375x_n+ 0.38125y_n -0.45625
p=0,33

Правило 2
x_n+1= 0.5x_n+  0.5y_n+0.50313
y_n+1= -0.5x_n+0.5y_n-0.50313
p=0,33

Правило 3
x_n+1= 0.5x_n+  0.5y_n+0.50313
y_n+1= -0.5x_n+0.5y_n+0.49688
p=0,34

Как всегда, по щелчку на картинке можно скачать изображение в полном размере.

Веточка

Вот такая красивая веточка получается, если при генерации IFS-фрактала задать два правила:

Правило 1
x_n+1= -0.65313x_n+0.14062y_n+0.2
y_n+1= 0.20625x_n+ 0.60625y_n-0.5875
p=0,5

Правило 2
x_n+1= 0.85x_n+  0.0875y_n+0.275
y_n+1= -0.2125x_n+0.8y_n+ 1.0625
p=0,5

Лист папоротника - IFS-фрактал

(можно скачать фрактал в размере 800x800)

IFS-фракталы строятся по следующему алгоритму:

Задаётся некоторое множество правил перехода текущей точки в следующую, у каждого правила - своя вероятность p его применения. Далее, начиная с точки (0;0), случайным образом выбирается правило и находится следующая точка, из неё получают следующую, и так далее.

Конкретно для этого рисунка набор правил был следующим:
Правило 1
x_n+1=0
y_n+1=0,16y_n
p=0,01

Правило 2
x_n+1=0,85x_n+0,04y_n
y_n+1=-0,04x_n+0,85y_n+1,6
p=0,85

Правило 3
x_n+1=0,2x_n-0,26y_n
y_n+1=0,23x_n+0,22y_n+1,6
p=0,07

Правило 4
x_n+1=-0,15x_n+0,28y_n
y_n+1=0,26x_n+0,24y_n+0,44
p=0,07

Этот, как и остальные представленные с блоге фракталы, построен с помощью программы Fractal Explorer

Жюлиа с кубом вместо квадрата

Это фрагмент множества Жюлиа, получающегося для итерационного процесса Z_n+1=Z_n³+С при С=0,66+0,5i

Щёлкнув по картинке, можно скачать её в полном размере.

Множество Жюлиа

Множество Жюлиа строится аналогично множеству Мандельброта, только величину C берут не с комплексной плоскости, а задаются ей вначале, для каждой же точки вычисляется число шагов, за которое последовательность итераций Z_n+1=Z_n²+С уйдёт из круга радиусом 2. 

Представленное здесь множество получается при C=0,31+0,47i .

При щелке на картинку, её можно скачать в разрешении 1024х768.

Неделя фракталов на Десяти буквах

Каждый день с 3 по 9 мая мы будем публиковать новую фрактальную картинку.

Та выглядит область Мандельброта в окрестности точки (0,2676553; 0,0040904):

Числовая пирамида

1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321

4

Число 4 - единственный квадрат, стоящий между парой простых чисел-близнецов.
Кроме того, это единственная степень двойки, обладающая данным свойством.