Из несчётного множества мировых обычаев и традиций, возможно, ни одно не сравнимо по элегантности и красоте с традицией сангаку - японской храмовой геометией. С 1639 по 1854 год Япония жила в жёсткой самоизоляции от Запада. Доступ ко всем формам западной культуры пресекался, и приток научных идей с Запада был эффективно сокращён. Именно в этот период изоляции и расцвела национальная разновидность математики.
Поклонники математики, обычно - самураи, купцы или крестьяне, могли решать многочисленные геометрические задачи, оформлять свои усилия на тонко раскрашенных деревянных дощечках и вывешивать эти изделия под крышами религиозных зданий. Изготовления этих сангаку, что дословно означает треугольник, могли быть проявлениями уважения - благодарности к руководящему духу - или же бросания вызова другим поклонникам: реши это, если сможешь!
В основном, сангаку имели дело с обычной евклидовой геометрией. Но задачи эти резко отличались от тех, что можно встретить в типичном курсе геометрии в высшей школе. Окружности и эллипсы играли в них гораздо более значимую роль, чем в западных задачах: окружности, вписанные в эллипсы, и эллипсы в окружностях. Некоторые из них весьма просты и могут быть решены студентами первого курса.
Другие же практически невероятны, и современные геометры неизменно штурмуют их с помощью продвинутых методов, включая вычисления и аффинные преобразования.
Источник
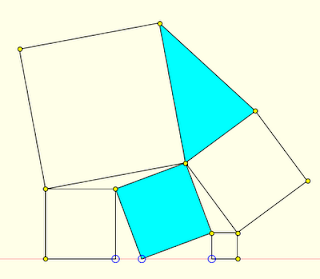
Вот пример задачи из сангаку:
Доказать, что при любом положении точек, обведённых синими кругами, площади бирюзовых фигур равны.
Здесь все четырёхугольники - квадраты.
Поклонники математики, обычно - самураи, купцы или крестьяне, могли решать многочисленные геометрические задачи, оформлять свои усилия на тонко раскрашенных деревянных дощечках и вывешивать эти изделия под крышами религиозных зданий. Изготовления этих сангаку, что дословно означает треугольник, могли быть проявлениями уважения - благодарности к руководящему духу - или же бросания вызова другим поклонникам: реши это, если сможешь!
В основном, сангаку имели дело с обычной евклидовой геометрией. Но задачи эти резко отличались от тех, что можно встретить в типичном курсе геометрии в высшей школе. Окружности и эллипсы играли в них гораздо более значимую роль, чем в западных задачах: окружности, вписанные в эллипсы, и эллипсы в окружностях. Некоторые из них весьма просты и могут быть решены студентами первого курса.
Другие же практически невероятны, и современные геометры неизменно штурмуют их с помощью продвинутых методов, включая вычисления и аффинные преобразования.
Источник
Вот пример задачи из сангаку:
Здесь все четырёхугольники - квадраты.
Комментариев нет:
Отправить комментарий