Вспомним, как определяются значения тригонометрических функций для произвольного t.
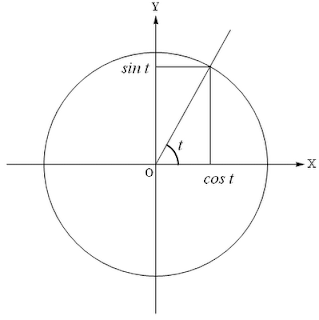
Если на единичной окружности, задаваемой уравнением x2+y2=1, отложить от оси ОХ против часовой стрелки угол t, то синусом его будет проекция соответствующей точки окружности на ось у, а косинусом - на ось х.
Заметим также, что угол t численно равен площади S вырезаемого им сектора окружности (примем, что при каждом переходе через полный круг, площадь всё увеличивается).
Гиперболические функции определяются аналогичным образом через гиперболу x2-y2=1 (как я рассказывал, гипербола - это не только график обратной пропорциональности)
Гиперболические синус и косинус будут проекциями точки пересечения луча, пущенного из начала координат с этой гиперболой на оси у и х, соответственно. Параметром t соответствующих функций берётся удвоенная площады S, заключённая между лучом, гиперболой и осью ОХ (если луч откладывается в нижнюю полуплоскость, берётся знак минус).


Комментариев нет:
Отправить комментарий