Тогда a+b=0
воскресенье, 7 ноября 2010 г.
Сумма двух иррациональных чисел
При решении задач на доказательство рациональности/иррациональности некоторого выражения школьники часто высказывают заблуждение: "если числа a и b - иррациональны, то a+b - также иррационально".
То, что на самом деле сумма двух иррациональных чисел вполне может быть числом рациональным, и даже целым, можно показать, взяв
Тогда a+b=0
Тогда a+b=0
Подписаться на:
Комментарии к сообщению (Atom)
Популярные сообщения
-
Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существуе...
-
Если вы хотите проверить, содержится ли ваш телефон, год рождения или номер дома среди уже вычисленных знаков числа пи, воспользуйтесь этой ...
-
Как рассказал наш читатель в комментарии к посту о целочисленном треугольнике , площадь четырёхугольника, вписанного в окружность, вычисляе...
-
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат... -
Приведённые квадратные уравнения легко решать по теореме Виета. Достаточно найти два числа такие, произведение которых равно свободному член...
-
WolframAlpha - мощный математический онлайн-калькулятор. Быстро выполняет любые расчёты, раскладывает на множители, переводит в другие си... -
Многих школьников, и не только, занимает вопрос: почему умножение и деление выполняются до сложения и вычитания? В рунете на этот вопрос н...
-
Ещё одна задачка про матрицы. Рассмотрим матрицы 3х3, элементами которых могут быть только нули, единицы и двойки. Всего таким матриц будет ...
-
Для числа 12 на математических часах я выбрал одну их наиболее парадоксальных формул, согласно которой сумма всего бесконечного множества на...
-
Давайте начнём новый, 2022й год с интересной задачи. Рассмотрим квадратную таблицу. Попробуем её заполнить натуральными числами так, чтобы с...
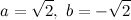
Прочитал и вспомнил, другое заблуждение, про то что произведение первых простых чисел + 1 -- простое число. Более подробно написал у себя в блоге: http://mmmkot.livejournal.com/5006.html
ОтветитьУдалитьО, да-да-да :) Ещё помню, когда впервые прочитал Эвклидово доказательство "произведением N первых простых чисел +1 должно быть простым или делиться на простое, большее P_N", удивлялся :)
ОтветитьУдалитьПриведите, пожалуйста, пример, когда сумма двух положительных иррациональных чисел равна рациональному числу. Именно положительных!!!
ОтветитьУдалитьхорошо, пусть $a=\sqrt{2}$, $b=2-\sqrt{2}$. a+b = 2
ОтветитьУдалить