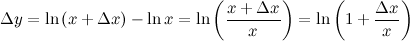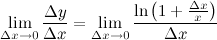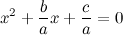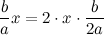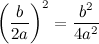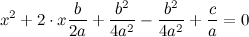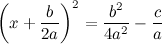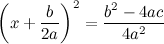На развлекательных сайтах время от времени публикуется и озадачивает посетителей следующий математический фокус.
Вас просят загадать двузначное число. Затем нужно переставить в нём цифры. И, наконец, от большего из чисел отнять меньшее.
Далее показывается таблица, в которой нужно найти полученную разность и сосредоточить внимание на цвете той ячейки.
А теперь выделите текст на странице, нажав Ctrl+A.
Она белая, верно?
Объяснение - под катом.
Вас просят загадать двузначное число. Затем нужно переставить в нём цифры. И, наконец, от большего из чисел отнять меньшее.
Далее показывается таблица, в которой нужно найти полученную разность и сосредоточить внимание на цвете той ячейки.
Она белая, верно?
Объяснение - под катом.

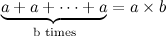
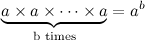
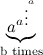
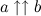
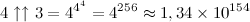
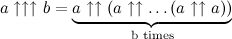
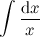 ,
, 
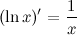
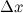 , то прирост зависимой можно вычислить по формуле:
, то прирост зависимой можно вычислить по формуле: