Второй замечательный предел.

Допустим, мы кладём 1 доллар на счёт под 100% годовых с выплатой процентов в конце срока. Через год у нас будет 2 доллара.

А что если на вклад будет начисляться по 50% каждые 6 месяцев? Тогда черед полгода у нас будет 1,5 доллара, а через год 1,5x1,5=2,25 доллара, что больше двух долларов.

А если каждый квартал вклад будет увеличиваться на 25%?
В конце первого квартала на счету будет 1,25 доллара. Через полгода 1,251,5625. Через девять месяцев - 1,5625x1,25=1,953125. А через год начислится 1,953125x1,25=2,44140625 - ещё больше, чем в предыдущем случае.

Будет ли получаемая сумма расти неограниченно с уменьшением сроков выплат процентов? Посмотрим, что будет с ежедневным начислением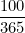  процента. По аналогии с предыдущими вычислениями можно получить, что сумма на счету составит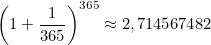
Рост по сравнению с ежеквартальным начислением незначительный.

Так вот, оказывается, что если продолжать уменьшать сроки между выплатами практически до нуля, вклад в конечном счёте увеличится в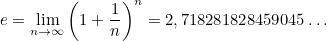 раз.

Число е играет важную роль в математике, в частности, в описании процессов, связанных с ростом.