Красивое доказательство того, что производная логарифма - это величина, обратная аргументу, показал Денис Сепетов:
Попробуем взять интеграл
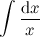 ,
, Сделаем замену переменной: x = et, dx = etdt
Получится простой интеграл:
Теперь вернувшись к подстановке получаем, что t = lnx.
Кстати, а если брать тот же самый интеграл другим методом, можно получить интересный софизм.



Комментариев нет:
Отправить комментарий