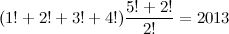С нового учебного года я начал читать два интересных блога по русскому языку. Блог ученика
Мир глазами человека и блог учителя
Оно вам надо!
В ученическом блоге даются советы по подготовке к олимпиаде "Русский медвежонок", объясняются некоторые неочевидные правила, публикуются новости из других областей науки. Почитав же учительский блог, я тоже узнал много нового и искренне обрадовался за учеников, с которыми работает такой замечательный педагог, как его автор.
Так вот, на днях я вспомнил об одной задаче, лежащей на стыке языка и математики. Когда-то мы вместе с форумчанами
Назвы и
Смекалки искали
самоописывающие выражения, то есть такие, количество букв в словесном описании которых равно их числовому значению. Как, например, в слове "
три" ровно 3 буквы, а во фразе "
два в кубе" букв 8.
После дальнейшего размышления оказалось, что есть способ построить подобное выражение для любого натурального числа, большего семи.
два в кубе = 8
трижды три = 9
дважды пять = 10
одиннадцать = 11
трижды четыре = 12
три плюс десять = 13
пять плюс девять = 14
треть сорока пяти = 15
восемь плюс восемь = 16
два плюс пятнадцать = 17
А теперь воспользуемся тем, что во фразе "плюс десять" ровно 10 букв и будем добавлять её к предыдущим выражениям:
два в кубе плюс десять = 18
трижды три плюс десять = 19
дважды пять плюс десять = 20
одиннадцать плюс десять = 21
......
дважды пять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять плюс десять = 100
......
Кстати, в англоязычной занимательной математике используется название "
честные числа" (
honest numbers). Там честными оказались числа 4, 8, 10, 11 и все, большие двенадцати.
Да, задача решена. Но не стало ли немного грустно от того, что решение оказалось таким простым и однообразным?
Чтобы продолжить наши математические развлечения, можно попробовать подбирать примеры, в которых бы не использовался плюс или в которых одно математическое действие не использовалось бы более раза.
Тогда выходит намного интереснее:
восьмое простое число = 19
антье корня из шестиста пяти = 24
логарифм десятичный ста дециллионов = 32
Приглашаю продолжить и заполнить пробелы!
По тегу "
самоописывающее" в блоге можно найти много других интересных конструкций, как математических, так и языковых..
 Читатели блога поделились ссылкой на чудесную анимацию. В ней для каждого натурального числа на экране располагаются соответствующее количество разноцветных точек. Расположение зависит от разложения числа на простые множители. Справа показан узор для числа 30.
Читатели блога поделились ссылкой на чудесную анимацию. В ней для каждого натурального числа на экране располагаются соответствующее количество разноцветных точек. Расположение зависит от разложения числа на простые множители. Справа показан узор для числа 30. Лежит куча песка. Если из кучи забрать одну песчинку, ку так кучей и останется. Но ведь продолжая забирать из кучи по песчине, в итоге от самой кучи тоже только песчинка и останется. Что же, выходит, песчинка тоже является кучей?
Лежит куча песка. Если из кучи забрать одну песчинку, ку так кучей и останется. Но ведь продолжая забирать из кучи по песчине, в итоге от самой кучи тоже только песчинка и останется. Что же, выходит, песчинка тоже является кучей?