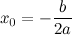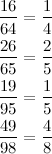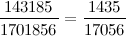Интересные числа, занимательные математические факты и удивительные конструкции. Узнавайте каждый день что-то новое!
понедельник, 30 мая 2011 г.
воскресенье, 29 мая 2011 г.
среда, 25 мая 2011 г.
вторник, 24 мая 2011 г.
Как нарисовать параболу от руки
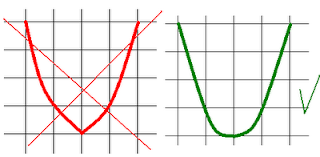
на клетчатом листе можно легко нарисовать параболу. Для этого сначала отмечаем точку - вершину параболы. Затем ставим новые точки, двигаясь вправо каждый раз на одну клетку, а вверх смещаемся на число клеток, равное последовательным нечётным числам: 1, 3, 5, 7 и т.д.
Далее так же получаем точки левой ветви параболы, и соединяем их плавной линией.
Следует учесть, что в вершине ветви должны плавно переходить друг в друга, а не образовывать угол.
воскресенье, 22 мая 2011 г.
Сангаку
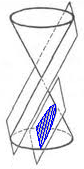
Из несчётного множества мировых обычаев и традиций, возможно, ни одно не сравнимо по элегантности и красоте с традицией сангаку - японской храмовой геометией. С 1639 по 1854 год Япония жила в жёсткой самоизоляции от Запада. Доступ ко всем формам западной культуры пресекался, и приток научных идей с Запада был эффективно сокращён. Именно в этот период изоляции и расцвела национальная разновидность математики.
Поклонники математики, обычно - самураи, купцы или крестьяне, могли решать многочисленные геометрические задачи, оформлять свои усилия на тонко раскрашенных деревянных дощечках и вывешивать эти изделия под крышами религиозных зданий. Изготовления этих сангаку, что дословно означает треугольник, могли быть проявлениями уважения - благодарности к руководящему духу - или же бросания вызова другим поклонникам: реши это, если сможешь!
В основном, сангаку имели дело с обычной евклидовой геометрией. Но задачи эти резко отличались от тех, что можно встретить в типичном курсе геометрии в высшей школе. Окружности и эллипсы играли в них гораздо более значимую роль, чем в западных задачах: окружности, вписанные в эллипсы, и эллипсы в окружностях. Некоторые из них весьма просты и могут быть решены студентами первого курса.
Другие же практически невероятны, и современные геометры неизменно штурмуют их с помощью продвинутых методов, включая вычисления и аффинные преобразования.
Источник
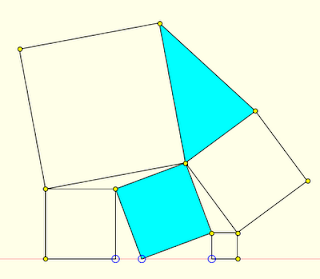
Вот пример задачи из сангаку:
Доказать, что при любом положении точек, обведённых синими кругами, площади бирюзовых фигур равны.
Здесь все четырёхугольники - квадраты.
Поклонники математики, обычно - самураи, купцы или крестьяне, могли решать многочисленные геометрические задачи, оформлять свои усилия на тонко раскрашенных деревянных дощечках и вывешивать эти изделия под крышами религиозных зданий. Изготовления этих сангаку, что дословно означает треугольник, могли быть проявлениями уважения - благодарности к руководящему духу - или же бросания вызова другим поклонникам: реши это, если сможешь!
В основном, сангаку имели дело с обычной евклидовой геометрией. Но задачи эти резко отличались от тех, что можно встретить в типичном курсе геометрии в высшей школе. Окружности и эллипсы играли в них гораздо более значимую роль, чем в западных задачах: окружности, вписанные в эллипсы, и эллипсы в окружностях. Некоторые из них весьма просты и могут быть решены студентами первого курса.
Другие же практически невероятны, и современные геометры неизменно штурмуют их с помощью продвинутых методов, включая вычисления и аффинные преобразования.
Источник
Вот пример задачи из сангаку:
Доказать, что при любом положении точек, обведённых синими кругами, площади бирюзовых фигур равны.
Здесь все четырёхугольники - квадраты.
понедельник, 16 мая 2011 г.
Домино из шахматной доски
Если из шахматной доски вырезать 2 угловых поля, лежащих на одной диагонали, то её станет невозможно полностью разрезать на "доминошки" 1x2.
Казалось бы, почему невозможно? Ведь остаётся 62 клетки, число чётное, и вполне может быть покрытое 31-й плиткой домино. Однако стоит вспомнить о раскраске. Среди оставшихся полей 30 белых и 32 чёрных. Доминошка же, как её ни располагай, будет всегда вмещать одно чёрное и одно белое поле. Таким образом, после того как вырежем из доски 30 плиток, останутся 2 несвязанные чёрные клетки.
Казалось бы, почему невозможно? Ведь остаётся 62 клетки, число чётное, и вполне может быть покрытое 31-й плиткой домино. Однако стоит вспомнить о раскраске. Среди оставшихся полей 30 белых и 32 чёрных. Доминошка же, как её ни располагай, будет всегда вмещать одно чёрное и одно белое поле. Таким образом, после того как вырежем из доски 30 плиток, останутся 2 несвязанные чёрные клетки.
воскресенье, 15 мая 2011 г.
суббота, 14 мая 2011 г.
воскресенье, 8 мая 2011 г.
Разбиения числителей и знаменателей в произведения
Несколько интересных дробей привёл наш читатель в ответ на пост о правильно-неправильных сокращениях:
Интересно, есть ли подобные дроби, у которых числитель и знаменатель разбиваются на одинаковое число множителей? (Этого я сам не знаю).
Интересно, есть ли подобные дроби, у которых числитель и знаменатель разбиваются на одинаковое число множителей? (Этого я сам не знаю).
суббота, 7 мая 2011 г.
Задачки
В задаче о представлении единицы в виде суммы четырёх аликвотных дробей нашими читателями из 14 способов найдено уже 7. Не хочу лишать удовольствия найти все разложения самостоятельно, а тем временем разовью в задачу ещё один пост блога.
Когда-то я писал о правильно-неправильном сокращении дроби
Можно получить верный результат, просто зачеркнув одинаковые цифры в числителе и знаменателе.
А сколько ещё существует дробей, обладающих таким свойством, у которых числитель и знаменатель - разные двузначные числа?
Когда-то я писал о правильно-неправильном сокращении дроби
Можно получить верный результат, просто зачеркнув одинаковые цифры в числителе и знаменателе.
А сколько ещё существует дробей, обладающих таким свойством, у которых числитель и знаменатель - разные двузначные числа?
пятница, 6 мая 2011 г.
Нечет + нечет = ... Нечет?
Да, оказывается, бывает и такое. Дело в том, что в математике нечётными могут быть не только числа, но и функции. Функция называется нечётной, если для любых допустимых значений переменной выполняется соотношение:
f(-x)=-f(x)
Таким образом, функция s(x), полученная как сумма двух нечётных функций f(x)+g(x) также будет нечётной:
s(-x)=f(-x)+g(-x)=-f(x)-g(x)=-(f(x)+g(x))=-s(x)
График нечётной функции симметричен относительно начала координат. Нечётными функциями являются прямая и обратная пропорциональности, кубическая парабола, синус, тангенс, котангенс и некоторые другие.
f(-x)=-f(x)
Таким образом, функция s(x), полученная как сумма двух нечётных функций f(x)+g(x) также будет нечётной:
s(-x)=f(-x)+g(-x)=-f(x)-g(x)=-(f(x)+g(x))=-s(x)
График нечётной функции симметричен относительно начала координат. Нечётными функциями являются прямая и обратная пропорциональности, кубическая парабола, синус, тангенс, котангенс и некоторые другие.
среда, 4 мая 2011 г.
Нарисовать окружность от руки
На клетчатой бумаге легко нарисовать окружность без циркуля. Для этого отметьте центр и 12 точек так, как показано на рисунке:

Расстояние от центра до каждой из точек равно 5 - они лежат на одной окружности. Через них можно провести плавную линию и от руки.

Расстояние от центра до каждой из точек равно 5 - они лежат на одной окружности. Через них можно провести плавную линию и от руки.
вторник, 3 мая 2011 г.
8 ферзей
Существует 92 способа расставить 8 ферзей на шахматной доске так, чтобы никакие два из них не били друг друга. Из этих способов только 12 - существенно различны, остальные же получаются из основных путём поворотов и отражений.


понедельник, 2 мая 2011 г.
Единица
Есть три способа представить единицу в виде суммы трёх аликвотных дробей:
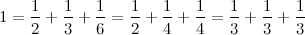
И только в одном из них все слагаемые различны.
А сколькими способами представляется единица в виде суммы четырёх аликвотных дробей?
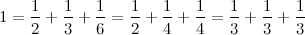
И только в одном из них все слагаемые различны.
А сколькими способами представляется единица в виде суммы четырёх аликвотных дробей?
Подписаться на:
Комментарии (Atom)
Популярные сообщения
-
Если вы хотите проверить, содержится ли ваш телефон, год рождения или номер дома среди уже вычисленных знаков числа пи, воспользуйтесь этой ...
-
Как рассказал наш читатель в комментарии к посту о целочисленном треугольнике , площадь четырёхугольника, вписанного в окружность, вычисляе...
-
Приведённые квадратные уравнения легко решать по теореме Виета. Достаточно найти два числа такие, произведение которых равно свободному член...
-
Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существуе...
-
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат...
-
Мантисса - это дробная часть числа. Операция взятия дробной части обозначается фигурными скобками. {5}=0 {4,37}=0,37 По определению, дро...
-
Площадь треугольника, зная его стороны, можно найти по формуле Герона. < Где a, b, c - стороны треугольника, а p - полупериметр. Для...
-
С нового учебного года я начал читать два интересных блога по русскому языку. Блог ученика Мир глазами человека и блог учителя Оно вам на...
-
Стабильно в первую пятёрку самых читаемых постов блога "Десять Букв" входит заметка о правильно-неправильном выносе из-под корня ...
-
Ещё одна задачка про матрицы. Рассмотрим матрицы 3х3, элементами которых могут быть только нули, единицы и двойки. Всего таким матриц будет ...
Темы
число
цифра
простые
геометрия
юмор
дроби
язык
степень
делимость
пи
методы
история
квадрат
самоописывающее
время
задача
система счисления
узор
корень
тригонометрия
структура
е
сайты
конструкция
формулы
игра
факториал
функции
приближение
программа
фрактал
комбинаторика
последовательность
график
память
логарифм
вероятность
палиндром
пределы
конкурс
треугольник
магический квадрат
неизвестное
правильно-неправильное действие
видео
интеграл
уравнение
комплексные
софизм
заблуждения
процесс
ряды
цитаты
книги
окружность
прогрессия
среднее
стереометрия
число фи
выражения
графы
матрица
проценты
разрезания
логика
парабола
символ
статистика
2014
Фибоначчи
клеточный автомат
кривая
производная
фокус
головоломка
действия
иллюзия
куб
шахматы
многоугольник
новости
оказывается
оригами
подобие
построение
сложение
термин
тетраэдр
топология