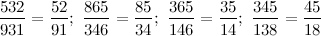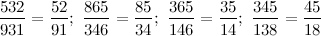Математика, как и любая другая наука, не стоит на месте, и давно устоявшиеся методы уступают место новым, более эффективным. Вот, например, самый древний алгоритм, алгоритм Эвклида, более двух тысяч лет успешно использующийся для нахождения наибольшего общего делителя двух чисел, оказался медленнее открытого в конце 60-х годов алгоритма Штейна.
Так и другие алгоритмы и методы, часто запутанные и нелогичные, как оказалось, могут быть заменены простыми операциями. В блоге иногда появлялись публикации на эту тему, так что частично подытожим их, при этом добавив кое-что новое.
Вычитание дробей
Чтобы из одной дроби вычесть другую, нужно разность знаменателей поделить на разность числителей.
Пример:
Сокращение дробей
Чтобы сократить дробь, нужно зачеркнуть одинаковые цифры в числителе и знаменателе
Примеры
Извлечение корня
Из-под корня можно вынести первую цифру числа.
Примеры:
Можно вынести целую часть смешанного числа.
Примеры:
Можно вынести вообще всё, кроме последней цифры, введя поправку (положительную для двузначных чисел и отрицательную для трёхзначных).
Примеры:
Умножение
Чтобы умножить число на 3, его первую цифру нужно перенести в конец.
Примеры: