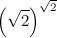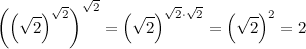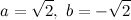Число 6 - наименьшее совершенное число. Оно, как и число 28 равно сумме всех собственных делителей
6:=1+2+3
Интересные числа, занимательные математические факты и удивительные конструкции. Узнавайте каждый день что-то новое!
вторник, 30 ноября 2010 г.
понедельник, 29 ноября 2010 г.
Одинаковые буквы
Буквы
Г, З, И, Л, М, П, С топологически одинаковы. Все они представляют собой согнутый отрезок без самопересечений.
Г, З, И, Л, М, П, С топологически одинаковы. Все они представляют собой согнутый отрезок без самопересечений.
воскресенье, 28 ноября 2010 г.
0
У цифры 0 есть две оси и один центр симметрии. В некоторых шрифтах этим свойством обладает и цифра 8, но в тех, где верхний кружок меньше нижнего, у неё всего-навсего одна ось симметрии.
суббота, 27 ноября 2010 г.
Форумная игра "Что? Где? Когда?"
На форуме умных людей Nazva.net пользователь Лев проводит игру "Что? Где? Когда?"
Ему удаётся создать атмосферу, максимально приближенную к телевизионной версии игры.Для участия в игре необходимо зарегистрироваться.
Вы можете по желанию занять сторону игроков или зрителей, в зависимости от того, хотите ли вы отвечать на вопросы или загадывать их.
В отличие от оригинальной игры, время на обсуждение вопроса составляет полчаса (30 минут), из-за учета особенностей форумной коммуникации. Оно может варьироваться в будущем.
Также отличие в том, что садиться за стол и вставать из-за него можно прямо посреди раунда.
Разумеется, под честное слово, в течение обсуждения запрещено пользоваться какими-либо иными источниками информации.
Очень рекомендую, если вам нравится загадывать или разгадывать интересные вопросы, принять участие! :)
Ему удаётся создать атмосферу, максимально приближенную к телевизионной версии игры.Для участия в игре необходимо зарегистрироваться.
Вы можете по желанию занять сторону игроков или зрителей, в зависимости от того, хотите ли вы отвечать на вопросы или загадывать их.
В отличие от оригинальной игры, время на обсуждение вопроса составляет полчаса (30 минут), из-за учета особенностей форумной коммуникации. Оно может варьироваться в будущем.
Также отличие в том, что садиться за стол и вставать из-за него можно прямо посреди раунда.
Разумеется, под честное слово, в течение обсуждения запрещено пользоваться какими-либо иными источниками информации.
Очень рекомендую, если вам нравится загадывать или разгадывать интересные вопросы, принять участие! :)
Air Traffic Control Arcade
Пишу новую флеш-игру - аркадный симулятор авиадиспетчера? попутно осваивая ActionScript 3.

На экран будут залетать самолёты, которые нужно провести до точек выхода.

Кроме опасности столкновения самих самолётов, мешать выполнить задание будут стаи птиц, грозы, ветер. Есть ещё пара нереализованных задумок.


На экран будут залетать самолёты, которые нужно провести до точек выхода.
Кроме опасности столкновения самих самолётов, мешать выполнить задание будут стаи птиц, грозы, ветер. Есть ещё пара нереализованных задумок.

среда, 24 ноября 2010 г.
Формулы перевода координат со сферы на плоскость
А вот и сами формулы перевода координат из системы широта-долгота в X-Y
Расстояние от точки с широтой B и долготой L до экватора откладывается на ось Y и равно широте в градусах, помноженной на длину одного градуса меридиана, т.е. на 111,2 км
Y=111,2*B
Расстояние от нулевого меридиана откладывается на ось X и равно долготе в градусах, помноженной на длину одного градуса параллели на широте точки. А та равна 111,2cosB
X=111,2*L*cos(B)
вторник, 23 ноября 2010 г.
Что бы это значило?
Ситуация:
Сидит человек за компьютером. Видно, что чем-то недоволен. Затем он перекрестил монитор, набрал что-то на клавиатуре, и, радостный, завершил работу.
На самом деле именно так со стороны выглядела ситуация, когда я писал программу перевода геодезических координат: широты и долготы на плоскость и забыл, какая из координат на какую ось отображается.
Сидит человек за компьютером. Видно, что чем-то недоволен. Затем он перекрестил монитор, набрал что-то на клавиатуре, и, радостный, завершил работу.
На самом деле именно так со стороны выглядела ситуация, когда я писал программу перевода геодезических координат: широты и долготы на плоскость и забыл, какая из координат на какую ось отображается.
понедельник, 22 ноября 2010 г.
воскресенье, 21 ноября 2010 г.
Геометрический паркет
Существует ровно 3 вида правильных многоугольников, которыми можно замостить плоскость: это правильный треугольник, четырёхугольник (квадрат) и шестиугольник.
суббота, 20 ноября 2010 г.
Умножение двузначного числа на 11
Чтобы двузначное число умножить на 11, сложите его первую и последнюю цифру. Если результат будет однозначным, впишите его между двумя цифрами первоначального числа, а если двузначным – прибавьте первую цифру результата к первой цифре первоначального числа, а вторую – впишите между цифрами.
Примеры:
45х11
Складываем 4+5=9. Поэтому результатом будет 495.
76х11
Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.
Математическое обоснование:
Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b
Примеры:
45х11
Складываем 4+5=9. Поэтому результатом будет 495.
76х11
Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.
Математическое обоснование:
Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b
четверг, 18 ноября 2010 г.
Простые близнецы
Хотя бесконечность множества простых чисел доказывается несложно, вопрос о конечности или бесконечности пар простых чисел-близнецов, т.е. таких, разность которых равна 2, до сих пор не решён.
вторник, 16 ноября 2010 г.
Сокращение вычислений
Чтобы проверить, является ли число простым, достаточно проверить делимость этого числа на все простые, не превосходящие корня из него.
Например, чтобы доказать простоту числа 101, достаточно показать, что оно не делится на 2, 3, 5 и 7.
Например, чтобы доказать простоту числа 101, достаточно показать, что оно не делится на 2, 3, 5 и 7.
понедельник, 15 ноября 2010 г.
Простое число на промежутке [n;2n]
Оказывается, между натуральным числом n, большем единицы, и удвоенным числом (2n) всегда найдётся простое число.
Эту теорему доказал Чебышев в 1850 году.
Эту теорему доказал Чебышев в 1850 году.
воскресенье, 14 ноября 2010 г.
n составных чисел подряд
Существуют сколь угодно длинные промежутки чисел, среди которых нет ни одного простого.
Например, все n чисел от (n+1)!+2 до (n+1)!+(n+1) - составные.
Например, все n чисел от (n+1)!+2 до (n+1)!+(n+1) - составные.
суббота, 13 ноября 2010 г.
1
По определению простого числа, у него ровно 2 делителя: 1 и само число.У составных же чисел делителей больше двух. Таким образом, число 1 - особенное, оно ни простое, ни составное.
четверг, 11 ноября 2010 г.
Простые числа в прогрессии
Любая арифметическая прогрессия с натуральными взаимно простыми первым членом и разностью включает бесконечное множество простых чисел.
среда, 10 ноября 2010 г.
Эвклидово доказательство бесконечности количества простых чисел
Допустим, простых чисел конечное количество. Но тогда, если их все перемножить, и прибавить единицу, получим число, которое не делится ни на одно из простых.
Вот на этом шаге часто, воспроизводя доказательство Эвклида, делают ошибку и говорят, что полученное число само является простым. Однако это не так: оно может быть или простым, или делящимся на некоторое простое число, большее максимального простого, входящего в произведение.
Действительно, числа
2+1=3
2*3+1=7
2*3*5+1=31
2*3*5*7+1=211
2*3*5*7*11+1=2311
- все простые, однако следующее:
2*3*5*7*11*13+1=30031 - составное, оно делится на 59.
Об этом математическом заблуждении, прочитав заметку о сумме иррациональных чисел, напомнил мне mmmkot.
Доказательство Эвклида очень хорошо иллюстрирует также принцип доказательства от противного: сначала мы предполагаем, что нечто верно, а затем показываем, к какому противоречию. приводит данное допущение.
Вот на этом шаге часто, воспроизводя доказательство Эвклида, делают ошибку и говорят, что полученное число само является простым. Однако это не так: оно может быть или простым, или делящимся на некоторое простое число, большее максимального простого, входящего в произведение.
Действительно, числа
2+1=3
2*3+1=7
2*3*5+1=31
2*3*5*7+1=211
2*3*5*7*11+1=2311
- все простые, однако следующее:
2*3*5*7*11*13+1=30031 - составное, оно делится на 59.
Об этом математическом заблуждении, прочитав заметку о сумме иррациональных чисел, напомнил мне mmmkot.
Доказательство Эвклида очень хорошо иллюстрирует также принцип доказательства от противного: сначала мы предполагаем, что нечто верно, а затем показываем, к какому противоречию. приводит данное допущение.
вторник, 9 ноября 2010 г.
Комплексное число в комплексной степени
А можно ли, возведя комплексное число в комплексную степень, получить действительное число?
Вот подсчитаем, чему равно ii
Для этого рассмотрим формулу Эйлера

Перенесём единицу вправо:
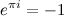
Теперь возведём левую и правую часть в степень i. Т.к. i2=-1, то
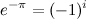
И теперь извлечём корень из левой и правой части:
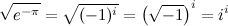
Таким образом,
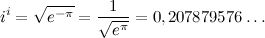
Итак, мнимое число во мнимой степени может давать действительный результат!
Вот подсчитаем, чему равно ii
Для этого рассмотрим формулу Эйлера
Перенесём единицу вправо:
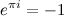
Теперь возведём левую и правую часть в степень i. Т.к. i2=-1, то
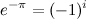
И теперь извлечём корень из левой и правой части:
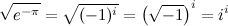
Таким образом,
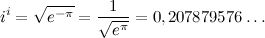
Итак, мнимое число во мнимой степени может давать действительный результат!
понедельник, 8 ноября 2010 г.
Иррациональная степень иррационального числа
А можно ли получить рациональное число, возведя иррациональное число в иррациональную степень?
Оказывается, тоже можно. Рассмотрим число
Если оно рационально, то задача решена. Если же нет (а на самом деле оно иррационально, но доказательство этого занимает солидный научный труд), то рассмотрим число
Которое является целым.
Оказывается, тоже можно. Рассмотрим число
Если оно рационально, то задача решена. Если же нет (а на самом деле оно иррационально, но доказательство этого занимает солидный научный труд), то рассмотрим число
Которое является целым.
воскресенье, 7 ноября 2010 г.
Сумма двух иррациональных чисел
При решении задач на доказательство рациональности/иррациональности некоторого выражения школьники часто высказывают заблуждение: "если числа a и b - иррациональны, то a+b - также иррационально".
То, что на самом деле сумма двух иррациональных чисел вполне может быть числом рациональным, и даже целым, можно показать, взяв
Тогда a+b=0
Тогда a+b=0
суббота, 6 ноября 2010 г.
Как ещё запомнить пи
Существует числовой стишок:
Надо только постараться и запомнить всё как есть — три, четырнадцать, пятнадцать, девяносто два и шесть.
Его указала в своём комментарии elka.
Есть ещё одна фраза, в которой количества букв в словах соответствуют цифрам:
Это я знаю и помню прекрасно: пи многие знаки мне лишни, напрасны
Надо только постараться и запомнить всё как есть — три, четырнадцать, пятнадцать, девяносто два и шесть.
Его указала в своём комментарии elka.
Есть ещё одна фраза, в которой количества букв в словах соответствуют цифрам:
Это я знаю и помню прекрасно: пи многие знаки мне лишни, напрасны
пятница, 5 ноября 2010 г.
Делимость на 7
Есть 164 шестизначных чисел, которые делятся на 7 при любом порядке своих цифр. Одно из них число 188111
Подробнее об этом - в решении задачи 3 Математических Маневров
Подробнее об этом - в решении задачи 3 Математических Маневров
четверг, 4 ноября 2010 г.
Подписаться на:
Комментарии (Atom)
Популярные сообщения
-
Если вы хотите проверить, содержится ли ваш телефон, год рождения или номер дома среди уже вычисленных знаков числа пи, воспользуйтесь этой ...
-
Приведённые квадратные уравнения легко решать по теореме Виета. Достаточно найти два числа такие, произведение которых равно свободному член...
-
Как рассказал наш читатель в комментарии к посту о целочисленном треугольнике , площадь четырёхугольника, вписанного в окружность, вычисляе...
-
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат...
-
Векторы можно складывать, вычитать, умножать на число. А перемножать векторы между собой можно даже двумя способами: скалярно и векторно. ...
-
Мантисса - это дробная часть числа. Операция взятия дробной части обозначается фигурными скобками. {5}=0 {4,37}=0,37 По определению, дро...
-
на клетчатом листе можно легко нарисовать параболу. Для этого сначала отмечаем точку - вершину параболы. Затем ставим новые точки, двигаясь ...
-
Способ разложения числа в цепную дробь с помощью калькулятора имеет ограничения точности. Но, оказывается, для квадратных корней существуе...
-
С нового учебного года я начал читать два интересных блога по русскому языку. Блог ученика Мир глазами человека и блог учителя Оно вам на...
-
Аликвотными называются обыкновенные дроби, числитель которых равен единице. Существует 2 способа представления дроби в виде суммы и один ...
Темы
число
цифра
простые
геометрия
юмор
дроби
язык
степень
делимость
пи
методы
история
квадрат
самоописывающее
время
задача
система счисления
узор
корень
тригонометрия
структура
е
сайты
конструкция
формулы
игра
факториал
функции
приближение
программа
фрактал
комбинаторика
последовательность
график
память
логарифм
вероятность
палиндром
пределы
конкурс
треугольник
магический квадрат
неизвестное
правильно-неправильное действие
видео
интеграл
уравнение
комплексные
софизм
заблуждения
процесс
ряды
цитаты
книги
окружность
прогрессия
среднее
стереометрия
число фи
выражения
графы
матрица
проценты
разрезания
логика
парабола
символ
статистика
2014
Фибоначчи
клеточный автомат
кривая
производная
фокус
головоломка
действия
иллюзия
куб
шахматы
многоугольник
новости
оказывается
оригами
подобие
построение
сложение
термин
тетраэдр
топология