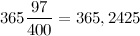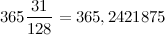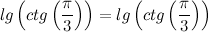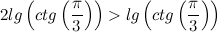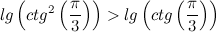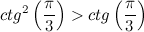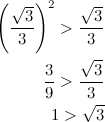Какое наибольшее число очков, которое можно выкинуть при броске двух стандартных игральных кубиков? Очевидно, 12 - когда оба кубика упадут шестёркой вверх.
Однако история сохранила одну необычную игру в кости, в которой исход партии решила случайность из разряда "одна на миллион".
Король Норвегии Олаф II и король Швеции, тоже Олаф, оспаривали друг у друга контроль над пограничным островом. Они решили разыграть его в кости (раньше я думал, что так они вообще решили обойтись без войны, а сейчас нашёл источник, в котором говорится, что сначала они, всё-таки, воевали, и за гораздо большие территории, а уже при мирных переговорах прибегли к игре).
По свидетельству хроники, шведский король выбросил две шестёрки и стал говорить, что норвежскому Олафу бесполезно даже пытаться. Но норвежский король бросил кубики - и у него выпало 2 шестёрки. Пока ничья.
Во втором заходе швед опять выбрасывает две шестёрки. Но когда норвежец бросил кубики, на одном выпала шестёрка, а другой раскололся пополам, и половинки дали в сумме 7 очков. 6+7=13. Шведу пришлось уступить.