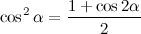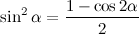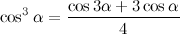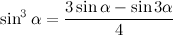Начнём последовательность с 1, 2, 3, а затем будем приписывать суммы попарных произведений последних трёх чисел в ней.
Сначала добавится число 11 = 1х2 + 2х3 + 1х3
Затем к последовательности 1, 2, 3, 11, добавится число 61 = 2х3 + 3х11 + 2х11
Получим: 1, 2, 3, 11, 61,...
Забавно, что числа 3, 11, 61 - являются простыми множителями числа 2013.
Далее она будет продолжаться как:
1, 2, 3, 11, 61, 887, 64535, ...
P.S. Надо же, ядватрижды без опечаток с первого раза написал слово последовательность :)
Сначала добавится число 11 = 1х2 + 2х3 + 1х3
Затем к последовательности 1, 2, 3, 11, добавится число 61 = 2х3 + 3х11 + 2х11
Получим: 1, 2, 3, 11, 61,...
Забавно, что числа 3, 11, 61 - являются простыми множителями числа 2013.
Далее она будет продолжаться как:
1, 2, 3, 11, 61, 887, 64535, ...
P.S. Надо же, я